Предположим, что во втором ящике было х кг гвоздей, тогда в первом ящике 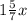 или
или 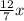 кг гвоздей, а в третьем
кг гвоздей, а в третьем 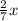 , также из условия задачи известно, что всего в трёх ящиках было 21 кг гвоздей
, также из условия задачи известно, что всего в трёх ящиках было 21 кг гвоздей
согласно этим данным составим и решим уравнение: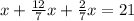
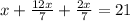 /·7
/·7
умножаем на 7 для того, чтобы избавиться от знаменателей
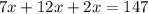
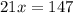
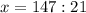
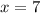 (кг) - гвоздей было во II ящике.
(кг) - гвоздей было во II ящике.
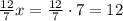 (кг) - гвоздей было в I ящике.
(кг) - гвоздей было в I ящике.
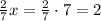 (кг) - гвоздей было в III ящике.
(кг) - гвоздей было в III ящике.
ответ: в первом ящике - 12 кг, во втором - 7 кг, а в третьем - 2 кг гвоздей.
Проверка:
12+7+2=21 (кг) - гвоздей всего.
У двоих братьев было вместе 112 р. После того как старший отдал младшему 14 р. у него осталось всё же больше денег , чем у младшего, но всего лишь на 10 р. Сколько денег было у каждого мальчика первоначально?
Примем
а, руб - количество денег у старшего брата,
в, руб - количество денег у младшего брата,
тогда
а+в=112
а-14=в+14+10
а=в+10+14+14=в+38
в+38+в=112
2*в=112-38=74
в=74/2=37 руб
а=37+38=75 руб
Проверим:
а+в=75+37=112 руб
75-14>37+14
61-51=10
75 руб - количество денег у старшего брата,
37руб - количество денег у младшего брата
Если a=41, то 2a=82 > 70.
2) Если хотя бы одна сторона должна быть целой, то: 36=3*12=3,6*10=4*9=4,5*8=5*7,2=6*6.
Всего 6 вариантов.
А если обе стороны должны быть целыми, то 3 варианта.
3) Сначала был прямоугольник x*y, x < y.
От него Оля отрезала 2 больших квадрата x*x.
y = 2x + k
Остался прямоугольник k*x, k < x. Отрезала квадрат k*k.
x = k + m
Остался прямоугольник m*k, m < k. Отрезала квадрат m*m.
k = m + n
Остался прямоугольник n*m, n < m. Отрезала квадрат n*n.
m = n + p
Получилось 3 меньших квадрата разной величины.
Остался p*n, который Оля разрезала на 2 квадрата 1*1.
Значит, p = 1; n = 2. Тогда
m = n + p = 2 + 1 = 3
k = m + n = 3 + 2 = 5
x = k + m = 5 + 3 = 8
y = 2x + k = 2*8 + 5 = 21
ответ: у Оли был прямоугольник 8*21 см.