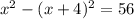
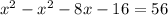
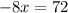
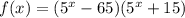
Уравнение касательной имеет вид:
,
где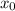 
— абсцисса точки графика функции 
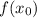, к которому проведена касательная 
.
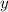Так как график касательной имеет вид график прямой линейной функции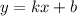 
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —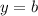 
Таким образом, касательная будет горизонтальной, если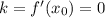 
Найдем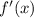 
:
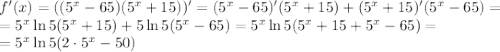
Найдем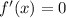 
:
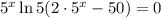
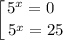
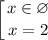
Следовательно,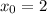 
— абсцисса точки графика функции 
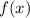, к которому проведена касательная .
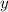Найдем значение :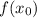
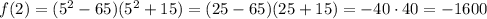
Таким образом,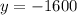 
— уравнение горизонтальной касательной к графику функции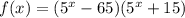
ответ: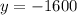
x+y=4
x^2-y^2=56
x=4-y
(4-y)^2-y^2=56
x=4-y
16-8y+y^2-y^2=56
-8y=40
x=4-y
y=-5
x=4+5
y=-5
x=9
(9;-5)