Найдем значение постоянной a. График параболы проходит через точку (2; 3), то есть:
3 = 2^2 * a;
a = 3/4.
То есть аналитически данная парабола задается следующим образом: y = 3x^2/4.
Пересечение происходит при одинаковых y. Приравнивая правые части уравнений, получаем:
3x^2/4 = 5 - x;
3x^2 + 4x - 20 = 0.
Получили квадратное уравнение. Решать его можно различными Во-первых, это дискриминант - базовая формула. Во-вторых, можно разложить на множители, зная один корень - 2 (по условию). Пойдем третьим путем: воспользуемся методом "переброски". Если в школе этот метод не изучали, то можно почитать о нем в интернете. Вводим t:
t^2 + 4t - 60 = 0;
Корни этого уравнения легко находим по теореме, обратной теореме Виета. Сумма корней равна -4, произведение - -60. Очевидно:
t = -10 ИЛИ t = 6. Тогда:
x = -10/3 ИЛИ x = 2.
Нас интересует x = -10/3. y(-10/3) = 3/4 * 100/9 = 25/3. Или же y(-10/3) = 5 - (-10/3) = 5 + 10/3 = 15/3 + 10/3 = 25/3.
ответ: (-10/3; 25/3).
Задача №1
Так как числа a,b,c обратно пропорциональны числам 3,4,5, то выполняется равенство:
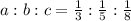
Преобразуем его, приведя дроби к общему знаменателю:
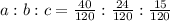
Пусть к - коэффициент пропорциональности. Тогда:
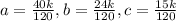
Найдем сумму чисел a,b,c:
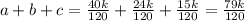
Для того, чтобы значение суммы было наименьшим целым, число к должно быть наименьшим числом, кратным 120. Это число 120.
Тогда наименьшее целое значение выражения 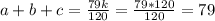
ответ: 79
====================================
Задача №2
Пусть первоначальная цена товара х рублей
1) После снижения: (30%=0,3)
х-0,3х= 0,7x(руб)
2) После повышения: (40%=0,4)
0,7х+0,4*0,7x = 0,7х+0,28х=0,98x (руб)
3) Разница: х-0,98х=0,02х=2% от х
ответ: уменьшилась на 2 процента