Пример смешанных дробей:
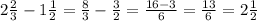
1.нужно убрать целую часть-перевести смешанную дробь в неправильную.
2.если знаменатели разный(у нас такой же случай), то приводим к общему знаменателю( в нашем случае общ. знаменатель- 6)
3. если одинаковые, тогда решаем рациональнее- вычисляем целые и дробные части отдельно:
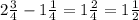
Пример обыкновенных дробей:
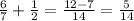
1. в данном случае, мы только приводим дроби к общ. знаменателю и далее вычисляем.
при сумме тех же дробей:
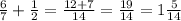
2. выполняем пункт 1 и выделяем целую часть: числитель делим на знаменатель.
Пример десятичных дробей:
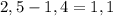-здесь можно вычитать не обращая внимания на запятую: 25-14=11, затем отделить запятую одну цифру справа налево.
ещё такой пример: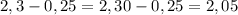
-здесь можно вычитать в столбик, только, чтобы запятая под запятой находились(смотри как это делается во вложении)
Ну в общем всё, Удачи)
ответ:
. дан отрезок ав. с циркуля и линейки разделите его на три равные части.
построение. 1) проведем отрезок ав;
2) из точки а проведем окружность произвольного радиуса, которая пересекает отрезок ав в точке д, а его продолжение за точку а - в точке с;
3) из точек с и д проводим окружности радиусом большим сд, пересекающиеся в точках м и n, через полученные точки проводим прямую мn, которая перпендикулярна прямой ав;
4) возьмем произвольную точку р прямой мn и проведем через нее прямую рк, перпендикулярную прямой мn; прямые ав и рк будут параллельны;
5) от начала р луча рм отложим три равных отрезка рр1, р1р2, р2р3, каждый из которых меньше отрезка ав;
6) через точки р3 и в проведем прямую, которая пересечет прямую мn в точке q;
7) проводим прямые р2q и р1q, которые и разделят отрезок ав на три равные части, аа1 = а1а2 = а2в. нетрудно доказать, используя подобие треугольников, что построенные части отрезка ав действительно равны.
пошаговое объяснение:
2)150-100=50 фонариков осталось развесить