ответ: Пусть скорость байдарки в стоячей воде = х км/ч. Тогда туристы плыли по течению со скоростью (х+3) км/ч, а против течения со скоростью (х-3) км/ч. Расстояние, которое туристы проплыли по течению = (2,4 х (умножить) (х+3)) км, а против течения (0,8 х (х-3)) км. Зная, что по течению туристы проплыли на 19,2 км больше, составим и решим уравнение.
2,4 х (х+3) - 0,8 х (х-3) = 19,2
2,4х +7,2 - 0,8 х +2,4 =19,2
1,6х +9,6 = 19,2
1,6х = 9,6
х = 6
Значит, скорость байдарки в стоячей воде 6 км/ч.
Пошаговое объяснение:
Пошаговое объяснение:
I вариант решения
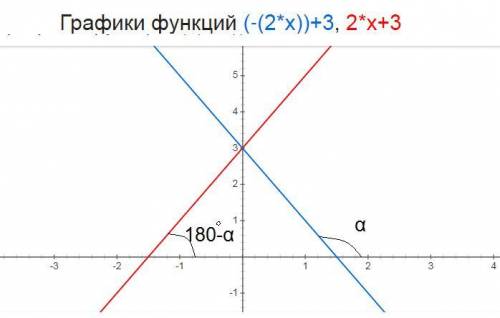
пусть прямая симметричная прямой y=-2x+3 имеет вид у=kx+b
найдем точки пересечения прямой y=-2x+3 с осями координат относительно оси ОУ
с осью ОХ у=0; -2x+3=0; 2x=3; x=1,5; (1,5;0)
с осью ОY x=0; y=3; (0;3)
так как прямые симметричны то
- они обе проходят через точку (0;3)
- симметричная прямая проходит через точку противоположную точке (1,5;0) точку (-1,5;0)
⇒ симметричная прямая проходит через точки (0;3) и (-1,5;0)
подставим координаты точки (0;3) в уравнение симметричной прямой у=kx+b координату точки (0;3)
получим 3=к*0+b; b=3
подставим координаты точки (-1,5;0) и значение b=3 в уравнение симметричной прямой у=kx+b получим
0=-1,5к+3 ; 1,5к=3; k=3/1,5=2
подставим b=1; k=2 в уравнение у=kx+b
у=2х+3
===============================================
II вариант решения - тригонометрический
так как прямые симметричны то их углы наклона к оси ОХ будут в сумме давать 180°
так как tg(180°-а)=-tga то угловые коэффициенты симметричных прямых будут к₁ и к₂ противоположными числами а значение b₁ и b₂ будут одинаковыми так как обе прямые пересекают ось ОУ в одной точке ⇒ к₂=-к₁=-(-2)=2; b₂=b₁=3
уравнение прямой симметричной прямой y=-2x+3 относительно оси ОУ
у=2х+3