Т.к. в любых двух вазах вместе лежит не более 5-х орехов, то в среднем в одной вазе должно находиться по 2,5 ореха. Начнём подбирать. Во все вазы положим по одному ореху. Потом будем добавлять орехи в вазы. В первую вазу можем положить не более 4-х орехов. И вот, если в первой вазе 4 ореха, то больше ни в какую вазу ни одного ореха не положить, т.к. окажется больше 5 орехов. А вот если в первой вазе будет 3 ореха, то во все остальные можно положить уже 2 ореха. В любых двух вазах окажется либо 4 ореха, либо 5. Что удовлетворяет условию. Больше уже в другие вазы не добавить. Если в первой вазе будет 2 ореха, то в остальные нельзя положить по 3 ореха. Только по два ореха. Да в одну вазу три, что приводит к предыдущему варианту.
Итак, в одной вазе 3 ореха, в остальных девяти по 2 ореха. Считаем: 3 + 9 × 2 = 21
Т.к. в любых двух вазах вместе лежит не более 5-х орехов, то в среднем в одной вазе должно находиться по 2,5 ореха. Начнём подбирать. Во все вазы положим по одному ореху. Потом будем добавлять орехи в вазы. В первую вазу можем положить не более 4-х орехов. И вот, если в первой вазе 4 ореха, то больше ни в какую вазу ни одного ореха не положить, т.к. окажется больше 5 орехов. А вот если в первой вазе будет 3 ореха, то во все остальные можно положить уже 2 ореха. В любых двух вазах окажется либо 4 ореха, либо 5. Что удовлетворяет условию. Больше уже в другие вазы не добавить. Если в первой вазе будет 2 ореха, то в остальные нельзя положить по 3 ореха. Только по два ореха. Да в одну вазу три, что приводит к предыдущему варианту.
Итак, в одной вазе 3 ореха, в остальных девяти по 2 ореха. Считаем: 3 + 9 × 2 = 21
ОДЗ:
1) 2x - 1 > 0; 2x > 1; x > 0,5
2) 2x - 1 ≠ 1; 2x ≠ 2; x ≠ 1
3) x² - 2x + 2 > 0; ⇔ (x² - 2x + 1) + 1 > 0;
(x - 1)² + 1 > 0 - выполняется при любых значениях х.
ОДЗ : x ∈ (0,5; 1) ∪ (1; +∞)
Метод интервалов с учётом ОДЗ
(0,5) ----------- [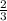 ] ++++++++++ (1) ------------>x
] ++++++++++ (1) ------------>x
ответ: x ∈ (0,5;2/3] ∪ (1; +∞)