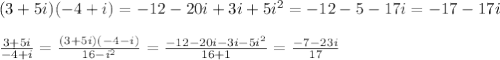
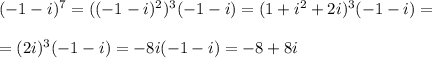
Пошаговое объяснение:
рассмотрим функцию f(x)=2x+(1/x²)-25,4
1) найдем производную
f'(x)=2-(2/x³)=(2x³-2)/x³=2(x³-1)/x³
правильный ответ первый
f'(x)=0 ; x³-1=0; x=1
при x>1 например x=2 ; f'(x)=2(8-1)/8=7/4>0 функция возрастает
при x∈(0;1) например 0.5 y'=2(0,125-1)/0,125<0 функция убывает
при х∈(-∞;0) например х=-1 ; f'(x)=2(-1-2)/-1>0 функция возрастает
2) f'(x)<0 при x∈(0;1)
3) на заданном интервале (0;1) функция убывает
при х=0,2 ; f(x)=2*0,2+(1/0,04)-25,4=0
так как при x∈(0;1) функция убывает а в точке х=0,2 функция равна 0 то это означает что при x∈(0;0,2) f(x)>0
2x+(1/x²)-25,4>0
2x+(1/x²)>25,4
что и требовалось доказать
4) для убывающей функции при х₁>x₂ f(x₁)<f(x₂)
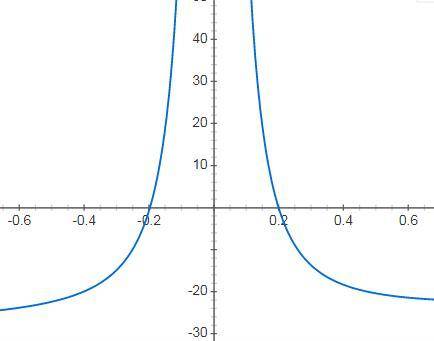
в качестве иллюстрации прилагается график функции
Пошаговое объяснение:
Вспомним, что такое периметр.
Периметр - это сумма длин всех сторон треугольника.
Найдем стороны треугольника ABC. Для этого запишем уравнение:
AB + BC + AC = 36 см
Так как AB = BC (боковые стороны р/б треугольника равны), то мы можем привести подобные слагаемые. Получим:
2AB + AC = 36 см
Найдем боковые стороны. Давайте пока "выкинем" из уравнения AC.
2AB = 36 см |:2
AB = 18 см (но так как боковые стороны не могут быть 18 см, мы 18 поделим еще раз на два)
AB = BC = 9 см
Найдем сторону AC:
AC = 36 - (AB + BC) = 36 - (9 + 9) = 36 - 18 = 18 см
Вспомним теорию:
Медиана - это отрезок, проведенный из вершины какого-либо угла к середине противолежащего отрезка.
Следовательно, точка D - середина отрезка AC, которая вдобавок еще и делит AC пополам. Отсюда можно найти AD = DC:
AC : 2 = 18 : 2 = 9 см
Теперь мы смело можем найти медиану BD: 30 - (9 + 9) = 12 см
Задача решена.