Общее число возможных элементарных исходов равно числу которыми можно извлечь 3 карты из 36:
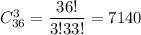
Подсчитаем число исходов, благоприятствующих данному событию:
Два туза выбираем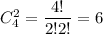 
а один валет 
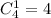Итого 
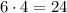
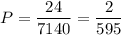— вероятность вытащить 2 туза и валет.
ВТОРОЙ
Первый туз можно достать с вероятностью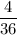 
, второй туз - 
а третий валет, с вероятностью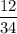 
, поскольку таких вариантов будет 12, {B1, T1, T2}, {B2,T1,T2}, {B3, T1,T2}, {B4,T1,T2}, {B1, T2, T3}, {B2,T2,T3}, {B3, T2,T3}, {B4,T2,T3}, {B1, T3, T4}, {B2,T3,T4}, {B3, T3,T4}, {B4,T3,T4}.
По теореме умножения: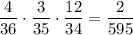 
Здравствуйте!
b. 0,72
Пошаговое объяснение:
У каждой лампочки только 2 режима:
- Лампочка горит
- Лампочка не горит (перегорела)
Других вариантов нет, также как и случаев, когда выполняется сразу оба режима. Поэтому сумма вероятностей то, что конкретная лампочка горит или не горит, всегда равна 1 (Она всегда либо горит, либо нет).
Из этого мы можем найти вероятность горения лампочки- она равна разности 1 и вероятности перегорания лампочки.
Тогда вероятность горения первой лампочки: 1- 0,2=0,8
Вероятность горения первой лампочки: 1- 0,1=0,9
Отметим, что горение одной лампочки не зависит от горения другой.
По теореме об умножении независимых вероятностей, вероятность выпадения двух нужных событий равна произведению событий:
P=0.9*0.8=0.72
y"=4x-x^3=x(4-x^2) \\методом интервалов приравниваем к нулю и
находим корни x(4-x^2)=0 x1=0;x2=2;x3=-2;
Где + возрастает,где - убывает.