Напишите разложение вектора х по векторам p q r,если х=(0,-2,1),р=(3,-4,2),q=(6,-1,5),r=(-3,-2,-6)

👇

Ответ:

Dydina5555521

27.01.2022

$\vec{x}= \alpha \vec{p}+ \beta \vec{q}+\gamma \vec{r}$
Где α,β и γ - некоторые коэффициенты в новом базике. Их и нужно найти.
Для этого перепишем верхнее уравнение в координатной форме:

$(0,-2,1)= \alpha (3,-4,2)+ \beta (6,-1,5)+\gamma (-3,-2,-6) \\ \\ (0,-2,1)= (3\alpha ,-4\alpha ,2\alpha )+ (6\beta,-\beta,5\beta)+ (-3\gamma,-2\gamma,-6\gamma) \\ \\ \left\{\begin{matrix} 3 \alpha +6 \beta -3\gamma=0
\\-4 \alpha - \beta -2 \gamma=-2
\\ 2 \alpha +5 \beta -6\gamma=1

\end{matrix}\right. \\ \\$

Решим методом Гаусса:

$\begin{pmatrix}
3 &6 &-3 &0 \\ 
 -4&-1 &-2 &-2 \\ 
 2& 5 &-6 &1 
\end{pmatrix}
\sim 
\begin{pmatrix}
1 &1 &3 &-1 \\ 
 -4&-1 &-2 &-2 \\ 
 2& 5 &-6 &1 
\end{pmatrix}
\sim \\ \\ \\ \sim\begin{pmatrix}
1 &1 &3 &-1 \\ 
 0&3 &10 &-6 \\ 
 0& 3 &-12 &3 
\end{pmatrix}
 \sim\begin{pmatrix}
1 &1 &3 &-1 \\ 
 0&3 &10 &-6 \\ 
 0& 0 &-22 &9 
\end{pmatrix}


$

$\left\{\begin{matrix}
 \alpha + \beta +3\gamma=-1\\ 3 \beta +10\gamma=-6
\\ -22\gamma=9

\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
 \alpha =-1- \beta -3\gamma\\ \beta= \frac{-6-10\gamma}{3} 
\\\gamma=- \frac{9}{22} 
\end{matrix}\right. 
\Leftrightarrow \left\{\begin{matrix}
 \alpha =-1- \beta + \frac{27}{22} \\ \beta= \frac{-6+ \frac{90}{22} }{3} 
\\\gamma=- \frac{9}{22} 
\end{matrix}\right. \\ \\$
$\Leftrightarrow \left\{\begin{matrix}
 \alpha =-1+\frac{7 }{11} + \frac{27}{22} \\ \\ \beta= -\frac{7 }{11} 
 \\ \\\gamma=- \frac{9}{22} 
\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}
 \alpha = \frac{19}{22} \\ \\ \beta= -\frac{7 }{11} 
\\ \\ \gamma=- \frac{9}{22} 
\end{matrix}\right. \\ \\ \\ OTBET: \ \vec{x}= \frac{19}{22}\vec{p} -\frac{7 }{11} \vec{q}- \frac{9}{22} \vec{r}$

4,5(29 оценок)

Открыть все ответы

Ответ:

Sambufer1

27.01.2022

1) $\displaystyle 4sin^{2}x-sin2x=3$

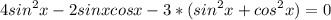
$\displaystyle 4sin^{2}x-2sinxcosx-3*(sin^{2}x+cos^{2}x)=0$

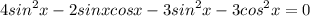
$\displaystyle 4sin^{2}x-2sinxcosx-3sin^{2}x-3cos^{2}x=0$

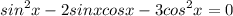
$\displaystyle sin^{2}x-2sinxcosx-3cos^{2}x=0$

Т.к. уравнение однородное,то мы можем поделить уравнение на cos²x≠0

$\displaystyle tg^{2}x-2tgx-3=0$

Пусть tgx = t, тогда

$\displaystyle t^{2}-2t-3=0$

$\displaystyle D = (-2)^{2} -4*1*(-3)=4+12=16=4^{2}$

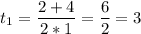
$\displaystyle t_{1}=\frac{2+4}{2*1}=\frac{6}{2}=3$

$\displaystyle t_{2}=\frac{2-4}{2*1}=-\frac{2}{2}=-1$

Вернёмся к замене

Если t = 3, тогда

tg x = 3

x = arctg(3)+пn, n∈Z

Если t = -1, тогда

tg x = -1

x = arctg(-1)+пn

x = -п/4 + пn, n∈Z

ответ: x = arctg(3)+пn, x = -п/4 + пn, n∈Z

2) $\displaystyle sin2x-cosx=0$

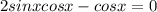
$\displaystyle 2sinxcosx-cosx=0$

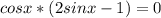
$\displaystyle cosx*(2sinx-1)=0$

Произведение равно нулю,когда хотя бы один из множителей равен нулю

а) cos x =0

x = п/2 + пn, n∈Z

б) 2sin x - 1 = 0

sin x = 0,5

x = (-1)ⁿ*arcsin(0,5)+пn

x = (-1)ⁿ*п/6+пn, n∈Z

ответ: x = п/2 + пn, x = (-1)ⁿ*п/6+пn, n∈Z

3) $\displaystyle sinx-\sqrt{3} cosx=0|:cosx\neq 0$

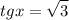
$\displaystyle tgx=\sqrt{3}$

x = arctg(√3)+пn

x = п/6 + пn, n∈Z

ответ: x = п/6 + пn, n∈Z

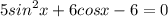
4) $\displaystyle 5sin^{2}x+6cosx-6=0$

$\displaystyle 5(1-cos^{2}x)+6cosx-6=0$

$\displaystyle 5-5cos^{2}x+6cosx-6=0|:(-1)$

$\displaystyle 5cos^{2}x-6cosx+1=0$

Пусть cosx = t, -1 ≤ t ≤ 1 тогда

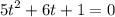
$\displaystyle 5t^{2}+6t+1=0$

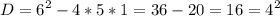
$\displaystyle D = 6^{2} -4*5*1=36-20=16=4^{2}$

$\displaystyle t_{1}=\frac{-6+4}{2*5}=-\frac{2}{10}=-0,2$

$\displaystyle t_{2}=\frac{-6-4}{2*5}=-\frac{10}{10}=-1$

Вернёмся к замене

Если t = -0,2, тогда

cos x = -0,2

x = ±arccos(-0,2)+2пn, n∈Z

Если t = -1, тогда

cos x = -1

x = п + 2пn, n∈Z

ответ: x = ±arccos(-0,2)+2пn, x = п + 2пn, n∈Z

4,7(37 оценок)

Ответ:

maxjk19

27.01.2022

Пошаговое объяснение:

Число попаданий в общем случае будет выражаться следующим образом:

$x = \frac {n - n_{0}}{k} \\$

где

х - число попаданий

n - общее число выстрелов

n0 - начальное (базовое) количество выстрелов

k - количество бонусных выстрелов, дающихся за 1 попадание.

И действительно: первые положенные выстрелы (n0) будут произведены в любом случае.

Если попаданий нет - выстрелов будет n0

если есть попадания - за каждое даётся по k дополнительных. И в последующие выстрелы - правило неизменно.

То есть общее число выстрелов (х) будет равно начальному числу выстрелов плюс число бонусов, равное произведению числа попаданий на количество бонусов за 1 попадание

$n= { n_{0} +k \cdot{x}} \\ k \cdot{x} = n - n_{0} \\ x = \frac {n - n_{0}}{k} \\ \\$