
(см. объяснение)
Пошаговое объяснение:
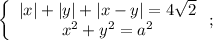
Заметим, что в первой строке системы нет параметра. Тогда выгодно построить ее в координатах 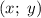 .
.
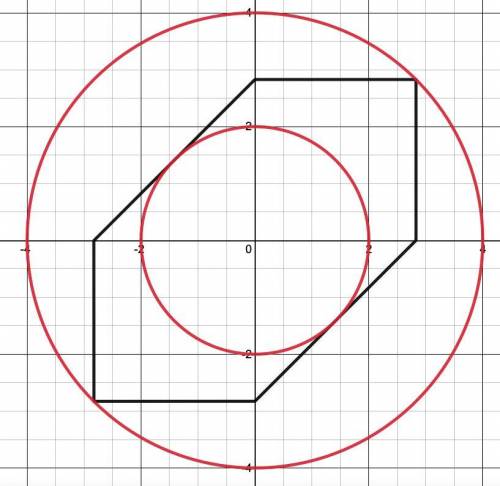
Вторая строка системы представляет из себя окружность, которая имеет фиксированный центр по координатам  и переменный радиус
и переменный радиус 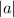 .
.
Будем менять радиус окружности до тех пор, пока не достигнем интересующей ситуации.
(см. прикрепленный файл)
В первом случае окружность касается прямых 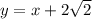 и
и 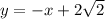 . Чтобы найти значение параметра здесь, удобнее всего будет воспользоваться формулой расстояния от точки до прямой:
. Чтобы найти значение параметра здесь, удобнее всего будет воспользоваться формулой расстояния от точки до прямой:
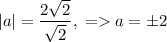
Во втором случае окружность проходит через точку 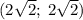 . Тогда подставим ее во вторую строку системы:
. Тогда подставим ее во вторую строку системы:

Получили, что при 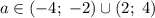 исходная система имеет ровно четыре различных решения.
исходная система имеет ровно четыре различных решения.
Так как по условию просят найти только положительные значения параметра, в ответ пишем  .
.
Задание выполнено!
1
Пошаговое объяснение:
5≡-1(mod3)
10≡1(mod3)⇒10³≡1³≡1(mod3)
5·10³≡-1·1≡-1(mod3)
2≡-1(mod3)⇒2¹⁹⁹⁵≡(-1)¹⁹⁹⁵(mod3)⇒-1(mod3)
2¹⁹⁹⁵ +5·10³ ≡-1+(-1)≡-2≡1(mod3)
. Можно использовать бином Ньютона или разложение выражений вида aⁿ+bⁿ где степень нечётное число или aⁿ-bⁿ где степень произвольное натуральное.
2¹⁹⁹⁵+1=(2+1)(2¹⁹⁹⁴-2¹⁹⁹³+2¹⁹⁹²-...+2²-2+1)=3*(2¹⁹⁹⁴-2¹⁹⁹³+2¹⁹⁹²-...+2²-2+1). Значит это число кратно трём. Пусть 2¹⁹⁹⁵+1=3A
5*10³-5=5*(10³-1)=5(10-1)(10²+10+1)=45(10²+10+1)
Значит и это число кратно трём. Пусть 5*10³-5=3B
2¹⁹⁹⁵ +5*10³=(2¹⁹⁹⁵+1)+(5*10³-5)+4=3A+3B+4=3(A+B+1)+1
Значит остаток 1