ответ: на движение навстречу друг другу, решаемые с рисунка.
существует два схожих между собою типа : на встречное движение и на погоню
(движение в одном направлении). следует иметь виду, что если происходит движение тел
навстречу друг другу со скоростями
1
v
и
2
v
, расстояние между которыми в момент начала
движения было
0 s
, то время, через какое эти тела встретятся, определяется по формуле
2 1
0
v v
s
t
.
если происходит движение тел со скоростями
1
v
и
2
v
в одном направлении (то есть одно
тело догоняет другое), то время, за которое одно тело догонит другое при
2 1
v v
, вычисляется по
формуле
2 1
0
v v
s
t
, где
0 s – расстояние между телами в начале движения.
1. из двух городов, расстояние между которыми равно 560 км, навстречу друг другу
одновременно выехали два автомобиля. через сколько часов автомобили встретятся, если их
скорости равны 65 км/ч и 75 км/ч?
решение.
4
140
560
65 75
560
2 1
0
v v
s
t
часа.
ответ: 4.
4. из городов a и b, расстояние между которыми равно 330 км, навстречу друг другу
одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города
b. найдите скорость автомобиля, выехавшего из города a. ответ дайте в км/ч.
решение. изобразим схематически эту .
автомобиль, выехавший из города а проехал
330180 150
км, значит его скорость была
50
3
150
v
км/ч.
ответ: 50.
7. расстояние между a и b равно 435 км. из города a в город b со
скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города b
выехал со скоростью 65 км/ч второй автомобиль. на каком расстоянии от города a автомобили
встретятся? ответ дайте в километрах.
решение. изобразим схематически эту .
пошаговое объяснение:
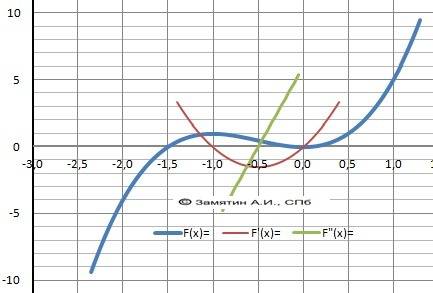
ДАНО F = 2*x³ + 3*x²
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет.
2. Пересечение с осью Х. F= x²*(2*x+3). Корни: х₁,₂ = 0, х₃ = -1,5.
3. Пересечение с осью У. F(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальной асимптоты - нет.
5. Исследование на чётность.F(-x)= - 2*x³ + 3*x² ≠ -F(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 6*x² + 6*х = 6*х*(х +1)= 0 .
Корни: х₁=0 , х₂ = -1.
Схема знаков производной.
_ (-∞)__(>0)__(x1=-1)___(<0)___(x2=0)__(<0)_____(+∞)__
7. Локальные экстремумы.
Максимум Ymax(-1)= 1, минимум – Ymin(0)=0.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;-1)∪(0;+∞) , убывает = Х∈[-1;0].
8. Вторая производная - Y"(x) = 12*x+6 = 6*(2x - 1)=0.
Корень производной - точка перегиба x = 0.5.
9. Выпуклая “горка» Х∈(-∞;0.5), Вогнутая – «ложка» Х∈(0.5;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(oo)F(x)/x = ∞. Наклонной асимптоты - нет
12. График в приложении.
1) Пусть площадь III комнаты - х м2, тогда площадь II комнаты - 3x м2, а площадь I комнаты - (3х+5) м2. Т.к. общая площадь равна 54 м2, получаем уравнение:
х+3х+3х+5=54
7х=54-5
7х=49
х=49:7
х=7 (это площадь III комнаты)
2) 7*3=21 (м2) - площадь II комнаты
3) 21+5=26 (м2) - площадь I комнаты