Пошаговое объяснение:
Из предыдущих выкладок известно, что a-c=4.
1) abc максимально. Цель - максимизировать старшие разряды.
Максимальное abc может быть получено так: в качестве a и b берем максимально возможные цифры, то есть a=9, b=9, тогда c=a-4=9-4=5.
2) abc минимально. Цель - минимизировать старшие разряды.
Минимальное abc может быть получено так: b можно взять равным 0, так как оно находится не на старшей позиции числа abc. Поскольку abc и cba трехзначные числа, то a>=1 и c>=1. Тогда если c = a-4, то a-4>=1, a>=5 - минимально возможное a=5, при котором c=1.
Пусть первое число арифметической прогресии равно а, тогда второе будет а + d, третье а +2d. Сумма а + а + d + а + 2d = 12
3а + 3d = 12
а + d = 4, следовательно а = 4 - d,
а + d = 4 (это второе число арифметической прогрессии)
при увеличении первого числа на 1, второго на 2 и третьего на 11 они составляют геометрическую прогрессию: 5-d; 6; 15+d.
Составим уравнение: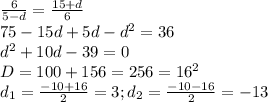
Так как арифметическая прогрессия убывающая, то подходит корень уравнения -13. Значит, первое число будет 4 - (-13) = 17; второе 4; третье 4 - 13 = -9.
Составим РС: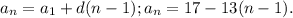 
- это арифметическая прогрессия.
Найдем РС для геометрической прогрессии: 18; 6; 2.
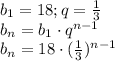
Т.к. мыши по условию могут быть любые, а всего мышей 3+3=6 ,то ищем число сочетаний двух из шести:
С выбора двух мышей , если они могут быть любого цвета.
ответ