Пошаговое объяснение:
1.
2cos^2(x/2)-1=1-2sin^2(x/2) (Формула косинуса двойного угла)
1-2sin^2(x/2)-5sin(x/2)-4=0
2sin^2(x/2)+5sinx(x/2)+3=0 (Квадратно уравнение)
D=25-24=1
sin(x/2)=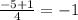
sin(x/2)=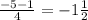
(Не возможно т.к. |sin(x/2)|≤1
sin(x/2)=-1
x/2=-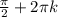
k∈Z
x=
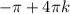k∈Z
2.
cos2(x)+cos^2(x)=5/4
2cos^2(x)-1+cos^2(x)=5/4
3cos^2(x)=5/4+1
3cos^2(x)=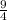
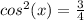
cos(x)=±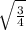
cos(x)=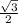
x=±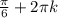
k∈Z
cos(x)=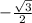
x=±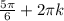
k∈Z
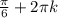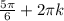ответ: x=± , x=± k∈Z.
3.
5sin^2(x)+3sin(x)*cos(x)-4=0
5sin^2(x)+3sin(x)*cos(x)-4sin^2(x)-4cos^2(x)=0
sin^2(x)+3sin(x)*cox(x)-4cos^2(x)=0 (разделим уравнения на cos^2(x))
tg^2(x)+3tg(x)-4=0
По т.Виета:
tg(x)=-4 (1)
tg(x)=1 (2)
(1)
tg(x)=-4
x=-arctg(4)+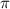
k k∈Z
(2)
tg(x)=1
x=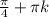
k∈Z
ответ: x=-arctg(4)+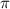k , x= 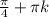k∈Z.
1) Начнём ставить ладьи по очереди. Для ладьи в первой строке есть 8 вариантов расстановки. Для ладьи во второй строке 7 (кроме того столбца, в котором стоит первая ладья), для ладьи из третьей - 6 и т.д
По правилу произведения получим 8×7×6×1=8!=40320 возможных расстановок.
2) На первом любая из 5 цифр может стоять, 5 вариантов.
На втором любая из оставшихся 4, 4 варианта.
На третьем любая из оставшихся 3, 3 варианта.
На 4-ом любая из оставшихся 2, 2 варинта.
На 5-ом только последняя неиспользованная.
5×4×3×2×1=120.
3) 6×5×4×3×2×1=720
4) У нас 7 человек в команде.
Сначала выберем капитана. Это можно сделать 7-ю
Выбираем вратаря. Осталось 6 человек (т.к капитан уже занят). Значит
Чтобы итоговое кол-во умножим полученные 6×7=42. ответ:42
5) комбираторика.
6) 5!/(5-3)!=5×4×3×2×1/2=20×3=60 (разных трёхцветных трёхполосных флагов)
7) …
8) Попробую предположить: Число
Когда Иванов попадет 50!/(4!*(50-4)!)-49!/(4!*(49-4)!)=18424
9) …
10) …
Дана функция y = (-x³/3)+2x²-3x-1.
Находим производную и приравниваем нулю:
y' = -x² + 4x - 3 = x² - 4x + 3 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-4)^2-4*1*3=16-4*3=16-12=4;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√4-(-4))/(2*1)=(2-(-4))/2=(2+4)/2=6/2=3;
x_2=(-√4-(-4))/(2*1)=(-2-(-4))/2=(-2+4)/2=2/2=1.
Получили 2 критические точки: х = 1 и х = 3 и три промежутка монотонности функции: (-∞; 1), (1; 3) и (3; +∞).
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = 0 1 2 3 4
y' = -3 0 1 0 -3
Минимум в точке х = 1, у = -2,3333.
Максимум в точке х = 3, у = -1.
Функция возрастает на промежутке (1; 3).
Функция убывает на промежутках (-∞; 1) ∪ (3; +∞).