Задание 1. Даны матрицы A,B,C.
1) В матрице A,B найти определитель;
2) Вычислить A-C
1)
7 2 4
det A = -3 9 -2 =
2 1 5
= 7·9·5 + 2·(-2)·2 + 4·(-3)·1 - 4·9·2 - 7·(-2)·1 - 2·(-3)·5 = 315 - 8 - 12 - 72 + 14 + 30 = 267
1 2 -4
det B= 6 5 1 =
-2 0 3
= 1·5·3 + 2·1·(-2) + (-4)·6·0 - (-4)·5·(-2) - 1·1·0 - 2·6·3 = 15 - 4 + 0 - 40 - 0 - 36 = -65
2) Решение и ответ на фото
Задание 2. Решить систему уравнений методом Гаусса. Решение на фото. Если подробно написать объяснение решений, это будет очень долго. И мне нравится метод Гаусса, сложно решать.
{x1 + x2 + x3 = 4
{5x1 + 3x2 + 2x3 = 1
{3x1 + 2x2 + 3x3 = -1
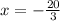
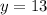
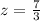
Задание 3.
Найдите производные следующих функций:
1)y=11x⁵+11
y'=55x⁴+0=55x⁴
2)
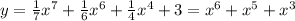
3 и 4, я не знаю как решить( поэтому оставлю как есть
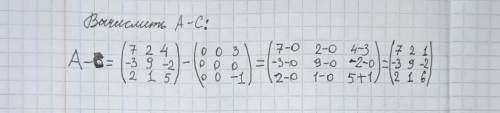
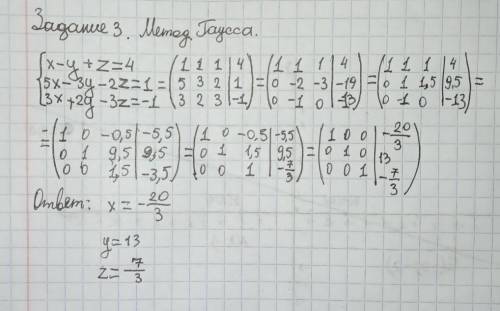
Пошаговое объяснение:
Вариант 1
1) Выполните деление с остатком: 478 : 15.
478:15 = 31 ост. 13
2) Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.
а=14 см
b=14*3=42 cм
S=a*b= 14*42=588 cм
3) Вычислите объем и площадь поверхности куба с ребром 3 см.
V куб= а³
V=3³=27 см³
4) Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.
а=18 см
b=18:2=9 см
с=9+11=20 см
V=a*b*c= 18*9*20=3240 см³
5) Чему равно делимое, если делитель равен 11, неполное частное – 7, а остаток – 6?
7*11+6=83
Делимое 83
6) Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.
1 га = 10 000 м²
6 га = 60 000 м²
S=a*b
150*b=60000
b=60000:150=400 м
Р=2*(150+400)=1100 м
7) Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).
560, 506, 605, 650
8) Сумма длин всех рёбер прямоугольного параллелепипеда равна 116 см, а два его измерения – 12 см и 11 см. Найдите третье измерение параллелепипеда.
4*(a+b+c)=116
a+b+c=116:4
a+b+c= 29
12+11+c=29
c= 6 см
Вариант 2
1) Выполните деление с остатком: 376 : 18.
376:18=20 остаток 16
2) Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.
а=21 см
b=21:3=7 см
S=a*b=21*7=147 см²
3) Вычислите объем и площадь поверхности куба с ребром 4 дм.
V=a³=4³=64 дм³
4) Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.
V=a*b*c
a=6 cм
b=6*5=30 cм
c=30-5=25 см
V=6*30*25=4500 cм³
пусть НОД = х, а НОК = х + 20
Очевидно, что если оба числа делятся на х, то и их НОК делится на х
х + 20 = kx
x(k - 1) = 20, x - делитель 20
1) x = 1 => a = 3; b = 7
НОД(3,7) = 1
НОК(3,7) = 21
21 - 1 = 20 - верно
или a = 1; b = 21
НОД(1, 21) = 1
НОК(1, 21) = 21
21 - 1 = 20 - верно
2) x = 2 => a = 2; b = 22
НОД(2, 22) = 2
НОК(2, 22) = 22
22 - 2 = 20 - верно
3) x = 4 => a = 4; b = 24
НОД(4, 24) = 4
НОК(4, 24) = 24
24 - 4 = 20 - верно
или a = 8; b = 12
НОД(8, 12) = 4
НОК(8, 12) = 24
24 - 4 = 20 - верно
4) x = 5 => a = 5; b = 25
НОД(5, 25) = 5
НОК(5, 25) = 25
25 - 5 = 20 - верно
5) x = 10 => a = 10; b = 30
НОД(10, 30) = 10
НОК(10, 30) = 30
30 - 10 = 20 - верно
6) x = 20 => a = 20; b = 40
НОД(20, 40) = 20
НОК(20, 40) = 40
40 - 20 = 20 - верно
ответ: (1, 21), (3, 7), (4, 24), (8, 12), (5, 25), (10, 30), (20, 40)