Задача № 1
Предположим, что в классе х (%) девочек, тогда мальчиков в классе (х+20) %, также примем во внимание, что всего в классе 100% учеников
согласно этим данным составим и решим уравнение:
х+х+20=100
2х+20=100
2х=100-20
2х=80
х=80:2
х=40 (%) - учеников в классе составляют девочки.
40+20=60 (%) - учеников в классе составляют мальчики.
ответ: мальчики составляют 60% учащихся класса, а девочки - 40%
Проверка:
40+60=100 (%) - всего учащихся в классе.
Задача № 2
составим пропорцию:
8% -100%
х% - 25%
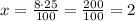 (%)
(%)
ответ: молоко содержит 2% жира.
Из всех прямоугольников, в которые можно поместить окружность, наименьшим будет тот, у которого все стороны равны диаметру этой окружности( действительно, все другие прямоугольники, подходящие для этого, могут быть получены "передвижением" сторон между прямых, содержащих две противоположные стороны).
Так как у окружности диаметр равен 6, то сторона искомого прямоугольника( в нашем случае, по доказанному ранее, квадрата) равна 2*3=6, откуда P=6*4=24.
2) Максимальный диаметр окружности, которую можно поместить в прямоугольник, равен меньшей из его сторон. В нашем случае получаем, что диаметр равен 4.
Какое максимальное количество точек может быть на окружности? Их может быть бесконечно много. Так как по условию задания получился многоугольник, то точек не меньше 3.
И чем больше точек отмечается, тем больше многоугольник по периметру приближается к длине окружности(по сути, наш многоугольник состоит из хорд, из каждого конца которой выходит лишь одна хорда. При этом длина хорды не больше длины дуги, которую она стягивает. При количестве точек, стремящимся к бесконечности, длины каждой хорды будет немногим меньше длины дуги, которую, она стягивает, а в сумме все дуги и дадут длину окружности.) Значит искомое значение равно