раскрывать модуль по определению...
в первом случае есть ограничения у≠0; х≠0, т.е. точки, лежащие на осях будут выколотыми; в остальном рассуждения для первых двух заданий очень похожи))
1) x < 0 ---> |y| / y = -x²
1a) y < 0 ---> -y / y = -x² ---> x² = 1 ---> x = -1 (т.е. в 3 четверти плоскости рисуем часть прямой (открытый луч) х=-1)
1b) y > 0 ---> y / y = -x² ---> x² = -1 нет решений (т.е. во 2 четверти плоскости будет пусто...)
2) x > 0 ---> |y| / y = x²
2a) y < 0 ---> -y / y = x² ---> x² = -1 нет решений (т.е. в 4 четверти плоскости будет пусто...)
2b) y > 0 ---> y / y = x² ---> x² = 1 ---> x = +1 (т.е. в 1 четверти плоскости рисуем часть прямой (открытый луч) х=1)
аналогично для второго равенства:
1) x < 0 ---> |y|y = -x²
1a) y < 0 ---> -y² = -x² ---> у² = х² ---> или у=х или у=-х (т.е. в 3 четверти плоскости рисуем часть прямой у=х -это биссектриса координатного угла; у=-х в 3 четверти не проходит...)
1b) y ≥ 0 ---> y² = -x² ---> у²+x² = 0 только точка (0;0) могла бы быть решением, но по условию x>0 ---> во 2 четверти нет решений...
2) x ≥ 0 ---> |y|y = x²
2a) y < 0 ---> -y² = x² ---> у²+x² = 0 только точка (0;0) является решением
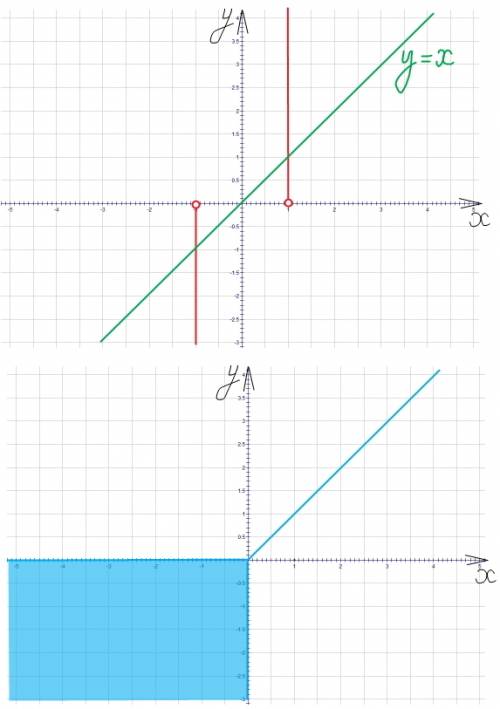
2b) y ≥ 0 ---> y² = x² ---> или у=х или у=-х (т.е. в 1 четверти плоскости рисуем часть прямой у=х -это биссектриса координатного угла; у=-х в 1 четверти не проходит...) на рисунке прямая зеленым цветом...
для третьего уравнения предлагаю повторить рассуждения самостоятельно (рисунок голубым цветом-это вся третья четверть, включая лежащие здесь части осей и часть прямой у=х)
169=x^2+144
x^2=25
x=5
sina=5/13
Пошаговое объяснение:
тут получается два подобных треугольника
первый с катетами - 1,7 м и 4 шага, а второй х (высота столба) и 12 шагов (4+80) т.к. эти треугольники подобны то их катеты относительны друг к другу и отсюда получаем 1,7 м /4 шага=х/12 шаг и отсюда выражаем х
х= 1,7 м * 3 = 5,1 метра высота столб линейки и транспортира опускается перпендикуляр, соединяющипусть дан правильный треугольник abc, его проэкция на плоскость def
центр треугольника лежит на пересечении медиан.
ad=10,be=15,cf=17
пусть t - середина стороны bc, пусть середина g стороны ef
тогда tg=1\2*(be+cf)=1\2*(15+17)=16
медианы в точке пересечения делтся 2: 1, начиная от вершины
пусть ax: xt=2: 1
пусть dh: hg=2: 1
тогда xh=1\3*af+2\3*tg=1\3*10+2\3*16=14
ответ: 14 дмй конец катета с лучом острого угла.ба
Пошаговое объяснение:
Сторона основания правильной треугольной пирамиды равна a. Боковое ребро образует с плоскостью основания угол 60°. Найдите радиус сферы, описанной около пирамиды.
Решение.
Пусть ABCP — данная правильная треугольная пирамида с вершиной P, AB = BC = AC = a, M — центр равностороннего треугольника ABC, ∠PAM = ∠PBM = ∠PCM = 60°. Поскольку пирамида правильная, PM — её высота. Из прямоугольного треугольника PAM находим, что
Поскольку центр описанной сферы равноудалён от вершин основания ABC, он лежит на прямой PM. Рассмотрим сечение пирамиды ABCP плоскостью, проходящей через точки A, P и середину L ребра BC. Получим треугольник APL, вершины A и P которого расположены на окружности с центром, лежащим на высоте PM, причём радиус R этой окружности равен радиусу сферы, описанной около пирамиды ABCP, и AM = 2ML.
Продолжим AL до пересечения с окружностью в точке Q. Поскольку ∠PAQ = 60° и PQ = AP, треугольник APQ — равносторонний, поэтому
Второй Пусть ABCP — данная правильная треугольная пирамида с вершиной P, AB = BC = AC = a, M — центр равностороннего треугольника ABC, ∠PAM = = ∠PBM = ∠PCM = 60°. Поскольку пирамида правильная, PM — её высота.
Из прямоугольного треугольника AMP находим, что
Поскольку центр описанной сферы равноудалён от вершин основания ABC, он лежит на прямой PM.
Продолжим высоту PM пирамиды до пересечения с описанной сферой в точке Q. Рассмотрим сечение пирамиды ABCP плоскостью, проходящей через точки A, P и Q. Поскольку PQ — диаметр окружности, радиус которой равен искомому радиусу R сферы, треугольник APQ — прямоугольный. Отрезок AM — его высота, проведённая из вершины прямого угла. Значит, AM2 = PM · MQ = PM(PQ − PM), или
В 1 четверти, при x > 0, y > 0, будут графики:
{ 1 = x^2; x = 1
{ y^2 = x^2; y = x (x > 0)
{ 2y = 2x; y = x (x > 0)
Пересечение трех графиков - это точка (1; 1).
Во 2 четверти, при x < 0, y > 0, будут графики:
{ 1 = -x^2
{ y^2 = -x^2
{ 2y = 0; y = 0
Эта система решений не имеет.
В 3 четверти, при x < 0; y < 0, будут графики:
{ -1 = -x^2; x = -1
{ -y^2 = -x^2; y = x (x < 0)
{ 0 = 0; x и y любые < 0
Пересечение этих графиков - это точка (-1; -1).
В 4 четверти, при x > 0, y < 0, будут графики:
{ -1 = x^2
{ -y^2 = x^2
{ 0 = 2x; x = 0
Эта система решений не имеет.
Итак, у нашей системы два решения: (1; 1) и (-1; -1).