постоянный положительный множитель можно выносить за знак модуля, поэтому уравнение примет вид:
|x+1|-|x-2|+3|x+2|=5
Универсальный метод решения уравнений с модулями - метод интервалов (метод расщепления)
Найдем нули подмодульных выражений:
x+1=0 => x=-1
x-2=0 => x=2
x+2=0 => x=-2
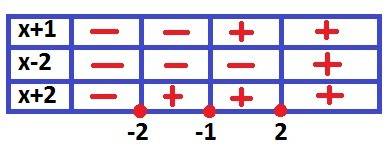
Составим небольшую таблицу, по которой определим знак каждого промежутка с пробной точки (см. рисунок)
Если в промежутке стоит +, то модуль просто опускается, если же -, то знаки под модулем меняются на противоположные
1 случай)
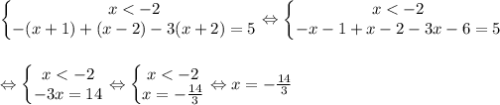
2 случай)
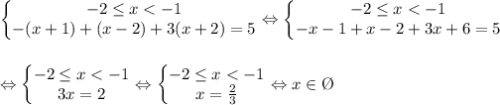
3 случай)
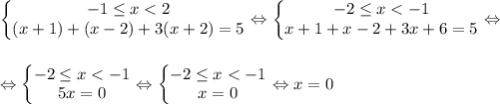
4 случай)
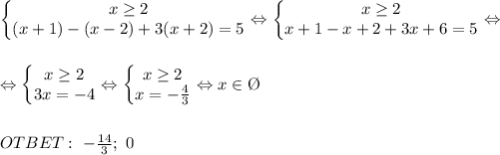
1) 82 * 1 = 82км скорый за 1ч
т.к. скорый двигался на 1ч дольше, значит
48 * 2 = 96км
96 + 82 = 178км за это время оба поезда
650 - 178 = 472 км - расстояние м/у ними
2) 48 * 3 = 144 км за 3ч товарный
82 * 2 = 164 км за 2ч скорый
144 + 164 = 308км оба поезда
650 - 308 = 342км - расстояние ч/з 3ч после выхода товарного
3) 82 *5 =410км за 5ч скорый
48 * 6 =288км товарный
288 + 410 = 698км оба поезда ч/з 5ч после выхода скорого
Это расстояние больше 650км, значит поезда уже встретились и удаляются друг от друга
698 - 650 = 48 км - такое расстояние м/у поездами ч/з 5ч после выхода скорого
Предположим, что х метров - первая часть верёвки, тогда 7х - вторая часть верёвки, также из условия задачи известно, что первоначальная длина верёвки 256 метров
согласно этим данным составим и решим уравнение:
х+7х=256
8х=256
х=256:8
х=32 (м) - длина I части верёвки.
7х=7·32=224 (м) - длина II части верёвки.
224-32=192 (м) - разница (на столько вторая часть длиннее первой части частей) - получилось равных частей верёвки.
2) 256:8=32 (м) - длина I части верёвки.
3) 32·7=224 (м) - длина II части верёвки.
4) 224-32=192 (м) - разница.
ответ: на 192 метра вторая часть верёвки длиннее первой части.
Проверка:
32+224=256 (м) - первоначальная длина верёвки.
в конце страницы написан ответ