46 + 14 = 56 : 7 = 31 + 37 = 6 : 2 = 40 + 38 = 18 : 3 =
57 - 14 = 4 * 5 = 80 - 57 = 9 * 2 = 80 - 69 = 27 + 52 =
24 : 6 = 36 + 63 = 56 : 8 = 7 + 42 = 81 : 9 = 51 + 37 =
5 * 3 = 82 - 23 = 4 * 2 = 5 - 1 = 4 * 2 = 80 - 71 =
34 + 51 = 72 : 9 = 8 3 + 36 = 24 : 8 = 64 + 9 = 14 : 2 =
41 + 21 = 3 * 9 = 95 - 76 = 9 * 5 = 93 - 87 = 8 * 4 =
50 + 34 = 24 : 4 =
Пошаговое объяснение:
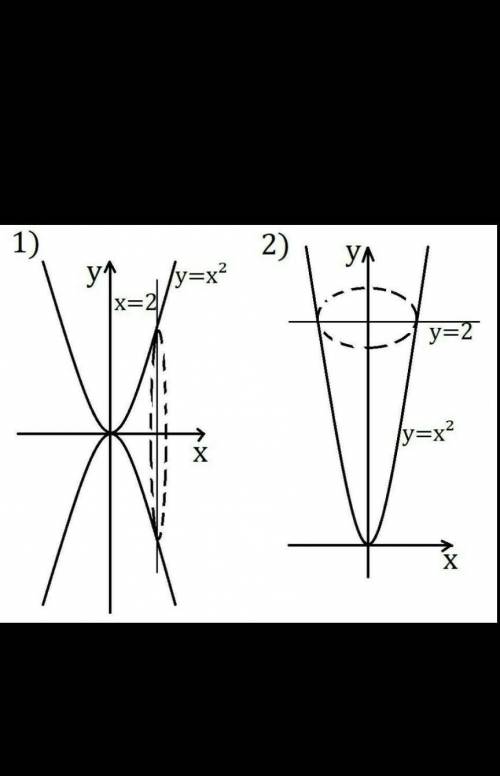
Объём тела, полученного при вращении вокруг оси Ox фигуры, ограниченной линиями y=x², x=0, x=2, равен:
\begin{gathered}\tt \displaystyle V=\pi \int\limits^2 _0 y^2 \; dx=\pi \int\limits^2 _0 x^4 \; dx=\pi \cdot \begin{pmatrix}\frac{x^5}5\end{pmatrix} \begin{vmatrix}\\ \\ \end{matrix} ^2 _0 =\\ \\ \\ =\pi \begin{pmatrix}\frac{2^5}5 -\frac{0^5}5\end{pmatrix} =\frac{32}5 \pi =6,\! 4\, \pi\end{gathered}
ответ: 6,4π.
2)
При x = -2, y = (-2)² = 4.
При x = 2, y = 2² = 4.
Надо найти объём тела, полученного при вращении вокруг оси Oy фигуры, ограниченной линиями y=x², y=4. \tt \displaystyle y=x^2 \rightarrow y_min =0y=x
2
→y
m
in=0
\begin{gathered}\tt \displaystyle V=\pi \int\limits^4 _0 x^2 \; dy=\pi \int\limits^4 _0 y \; dy=\pi \cdot \begin{pmatrix}\frac{y^2}2\end{pmatrix} \begin{vmatrix}\\ \\ \end{matrix} ^4 _0 =\\ \\ \\ =\pi \begin{pmatrix}\frac{4^2}2 -\frac{0^2}2\end{pmatrix} =8\pi \end{gathered}
ответ: 8π.
ответ: 1
Пошаговое объяснение:
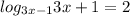; ОДЗ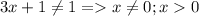 
; 
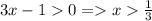
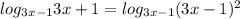
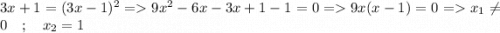исходя из ОДЗ ответ будет только x=1
20-14=6
9*9=81
16:4=4
25+6=31
50-20=30
22:11=2
5*10=50
12-5=7
32+8=40