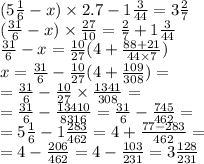
На каждой клетке доски размером 9×9 сидит жук, По свистку каждый из жуков переползает в одну из соседних по диагонали клеток. При этом в некоторых клетках может оказаться больше одного жука, а некоторые клетки окажутся незанятыми.
Докажите, что при этом незанятых клеток будет не меньше 9.На клетчатой бумаге даны произвольные n клеток. Докажите, что из них можно выбрать не менее n/4 клеток, не имеющих общих точекПлоскость раскрашена в три цвета. Докажите, что найдутся две точки одного цвета, расстояние между которыми равно 1.В левый нижний угол шахматной доски 8×8 поставлено в форме квадрата 3×3 девять фишек. Фишка может прыгать на свободное поле через рядом стоящую фишку, то есть симметрично отражаться относительно её центра (прыгать можно по вертикали, горизонтали и диагонали). Можно ли за некоторое количество таких ходов поставить все фишки вновь в форме квадрата 3×3, но в другом углу:
а) левом верхнем,
б) правом верхнем?
Памойму правильно если не правильно зделайте отметить нарушения.
Пошаговое объяснение:
(х-0,3)(6х-1)(5-2х)>0
корни уравнения (х-0,3)(6х-1)(5-2х)=0
x₁ = 1 /6; x ₂ = 0,3; х₃= 2,5
наносим их на числовую ось и смотрим значение функции на каждом интервале
(-∞; 1/6)
х₀ = 0; f(x₀) = f(0) = (0-0.3)(0-1)(5-0) = 0.15 > 0 интервал х < 1/6 подходит
(1/6; 0,3)
х₀ = 3/15 (например) считать не буду, просто посмотрю знаки, получится
f(x₀) < 0 не подходит
(0,3; 2,5)
x₀ = 1 (например). тоже просто знаки посмотрим, получим
f(x₀) > 0 подходит
(2,5; +∞)
x₀ = 3 (например). тоже просто знаки посмотрим, получим
f(x₀) = f(3) < 0 не подходит
таким образом имеем решение
х ∈ (-∞; 1/6) ∪ (0,3; 2,5)