первый рабочий
производительность х дет/мин
за время t+27 мин
половина задания x (t+27) =36 дет ; t=36/x-27 (1)
второй рабочий
производительность у дет/мин
за время t мин
половина задания y*t =36 дет ; t=36/y (2)
приравняем (1) и(2)
36/x-27 =36/у (3)
первый рабочий
полное время работы t1+27 мин
выпонено 72-4=68 деталей ; x*(t1+27)=68 ; t1=68/x-27 (4)
второй рабочий
полное время работы t1 мин
выполнено 72+4=76 деталей ; y*t1=76 ; t1=76/y (5)
приравняем (4) и(5)
68/x-27 =76/y (6)
решим систему уравнений (3) и(6) с двумя неизвестными
{ 36/x-27 =36/у
{ 68/x-27 =76/y
х=4/15
у=1/3
производительность
первого х=4/15 дет/мин = 16 дет/ час
второго у=1/3 дет/мин = 20 дет/час
3584
Пошаговое объяснение:
Пусть в сборнике n задач, тогда:
За 1 день решено: n/2+1
За 2 день решено: n/4+2
За 3 день решено: n/8+3
...
За 7 день решено: n/2^7+7
Сложим решенные за все дни задачи, причём дроби вида n/2^k (k - от 1 до 7) отделим от вторых слагаемых каждого дня:
(n/2+n/4+...+n/256)+(1+2+...+7)=n
Вынесем n из первой скобки:
n*(1/2+1/4+...+1/256)+(1+2+...+7)=n
Первая скобка (без n) - сумма первых семи членов геометрической прогрессии со знаменателем 1/2. 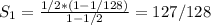
Вторая скобка - сумма первых семи членов арифметической прогрессии с разностью 1 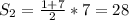
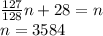
11 <х <25
Чётные: 12, 14, 16, 18, 20, 22, 24.
Нечётные: 13, 15, 17, 19, 21, 23.
66 <х <96
Чётные: 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94.
Нечётные: 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95.
45 <х <79
Чётные: 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78.
Нечётные: 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77.