Пошаговое объяснение:
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Используя эту формулу, решается задача 1) и 2) - ответами в обоих будет число 24. Для задачи 3) введем формулу (на картинке), где m - количество элементов в конечной выборке (т.е. то кол-во мужчин, которые садятся на скамейку), а n - кол-во элементов массива(кол-во свободных на скамейке мест). Подставив все величины в формулу, получим :
C =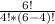 
= 15 возможностей их различной посадки
Разобравшись с яблоками, Чебурашка пошел в гости к Крокодилу Гене пить чай. Гена
отправил Чебурашку за вареньем в погреб. В погребе 11 банок облепихового варенья, 8 банок яблочного, 6 банок рябинового. Только вот Чебурашка не спросил Гену, сколько банок варенья нужно принести, а еще не взял с собой фонарик, поэтому ему пришлось выбирать варенье в темноте. Определите, какое максимальное количество банок Чебурашке нужно вынести из погреба, чтобы быть уверенным, что там останется еще хотя бы 4 банки одного сорта варенья и 3 банки другого сорта?
ответ 3
2 + 5 = 7 частей всего
140 : 7 = 20 одна часть
20 • 2 = 40
20 • 5 = 100
40 : 100
б) 2 + 12 = 14 частей всего
140 : 14 = 10 одна часть
10 • 2 = 20
10 • 12 = 120
20 : 120