Задание: раскройте скобки и у выражение
a) (2y+z) - (z-2y) = 2y+z-z+2y=4y.
б) (х+3) - (5х - 7) = x+3-5x+7=10-4x.
в) (2а - 1) + (3 - 4а) = 2a-1+3-4a=2-2a.
У ВЫРАЖЕНИЕ:
а) 2(a+b) + 3(a+b) + 2a =2a+2b+3a+3b+2a=7a+5b.
б) 5(x - z) - 2(x+z) =5x-5z-2x-2z=3x-7z.
в) 2(2r - 3s) - 3(r - 2s) =4r-6s-3r+6s=r.
г) 6(2a + c) + 2(6a - c) - 4c = 12a+6c+12a-2c-4c=24a+2c.
У а) b(m - 7) - 7b =bm-7b-7b=bm-14b.
б) x(c + 1) + c(x - 1) = xc+x+cx-c=2cx+x-c.
в) y(x - 4) + x(3 - y) = yx-4y+3x-xy=3x-4y.
Пошаговое объяснение:
Задание: раскройте скобки и у выражение
a) (2y+z) - (z-2y) = 2y+z-z+2y=4y.
б) (х+3) - (5х - 7) = x+3-5x+7=10-4x.
в) (2а - 1) + (3 - 4а) = 2a-1+3-4a=2-2a.
У ВЫРАЖЕНИЕ:
а) 2(a+b) + 3(a+b) + 2a =2a+2b+3a+3b+2a=7a+5b.
б) 5(x - z) - 2(x+z) =5x-5z-2x-2z=3x-7z.
в) 2(2r - 3s) - 3(r - 2s) =4r-6s-3r+6s=r.
г) 6(2a + c) + 2(6a - c) - 4c = 12a+6c+12a-2c-4c=24a+2c.
У а) b(m - 7) - 7b =bm-7b-7b=bm-14b.
б) x(c + 1) + c(x - 1) = xc+x+cx-c=2cx+x-c.
в) y(x - 4) + x(3 - y) = yx-4y+3x-xy=3x-4y.
Подробнее - на -
Пошаговое объяснение:
Предварительный Тест 1
Аксиомы стереометрии
Вариант 1
1
Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.
1) АВС 2) DBC 3) DAB 4) DAC
2
Каким плоскостям принадлежит точка К?
1) АВС и ABD
2) ABD и BCD
3) ACD и ABD
4) ABC и BCD
3
Выберите верные высказывания:
1) Любые три точки лежат в одной плоскости.
2) Если центр окружности и ее точка лежат в плоскости, то и вся окружность лежит в этой плоскости.
3) Через три точки, лежащих на прямой, проходит только одна плоскость.
4) Через две пересекающихся прямые проходит плоскость , и притом только одна.
а)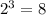 - а это уже палиндром
- а это уже палиндром
б) Сначала построим палиндром, кратный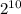
Пусть A - число из цифр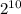 , записанных в обратном порядке (очевидно, что
, записанных в обратном порядке (очевидно, что 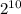 не оканчивается на 0 (иначе
не оканчивается на 0 (иначе 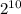 кратно 5), а значит A существует). Пусть также число цифр A равно n.
кратно 5), а значит A существует). Пусть также число цифр A равно n.
Тогда искомое число можно получить записав подряд число A, 10 нулей и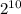 . И правда, это число равно
. И правда, это число равно 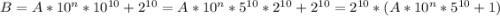 - кратно
- кратно 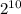
Записав 3 раза подряд число B, получим палиндром, кратный 3. И правда: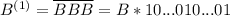 . Сумма цифр
. Сумма цифр 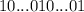 равна 3, а значит число кратно 3, а значит
равна 3, а значит число кратно 3, а значит 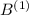 кратно
кратно 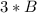 . Повторив эту операцию уже с числом
. Повторив эту операцию уже с числом 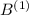 , получим
, получим 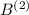 , кратное уже
, кратное уже  . Наконец на 10ом шаге получим палиндром
. Наконец на 10ом шаге получим палиндром 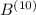 , кратный
, кратный 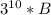 .
.
Т.к. B кратно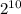 , то
, то 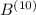 кратно
кратно  =
=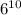
А значит палиндром, удовлетворяющий условию, существует.
Ч.т.д.