120+130=250т 2) 540-250=290т 3)290:2=145т 4)145+120=265т бензина осталось на заправочной станции
1971
Пошаговое объяснение:
Очевидно, x < 2025. Значит, x содержит не более 4 цифр.
Известно. что число и сумма его цифр дают одинаковые остатки при делении на 9. Обозначим этот остаток d. Для каких-то целых n и m выполняются соотношения x = 9n + d, S(x) = 9m + d. Подставляем в уравнение:
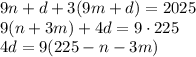
Правая часть этого равенства делится на 9, тогда и левая должна делиться, а тогда d = 0, то есть x и S(x) делятся на 9.
Есть 4 варианта для S(x): 9, 18, 27 и 36 - большую сумму цифр для не более чем четырехзначного числа не получить. Подставляя их в уравнение, находим x = 2025 - 3S(x), получается 1998, 1971, 1944 и 1917 соответственно. Все значения, кроме 1971, не подходят: при них сумма цифр отличается от той, которую мы подставляли.
Пошаговое объяснение:
1)
2 2/3(1 1/8x + 3/4) - (4x+1,5)=0
8/3*(9/8x + 3/4) - 4x - 1,5 = 0
3x + 2 - 4x - 1,5 = 0
-x + 0,5 = 0
x = 0,5
2)
2 1/7(2 1/3x - 1 2/5) - 3(2x-1)=9
15/7*(7/3x - 7/5) - 6x + 3 = 9
5x - 3 - 6x + 3 = 9
-x = 9
x = -9
3)
1 3/7(1 2/5x - 3 1/2)+0,7(5x-3)=9,4
10/7*(7/5x - 7/2) + 3,5x - 2,1 = 9,4
2x - 5 + 3,5x - 2,1 = 9,4
5,5x - 7,1 = 9,4
5,5x = 9,4 + 7,1
5,5x = 16,5
x = 16,5 : 5,5
x = 3
4)
5 1/3(2 1/4x+3/8) - 1,5(7x+4)=2
16/3*(9/4x + 3/8) - 10,5x - 6 = 2
12x + 2 - 10,5x - 6 = 2
1,5x - 4 = 2
1,5x = 2 + 4
1,5x = 6
x = 6 : 1,5
x = 4
265т бензина было 120+130=250
540-250=290
290÷2=145
145+120=265