Наибольшей общий делитель: 250 и 300; 36 и 72; 42 и 63; 60 и 150. наименьшее общее кратное: 2 и 3; 6 и 18; 4 и 6; 15 и 25; 12 и 18.

👇

Увидеть ответ

Ответ:

margo1084

11.01.2023

НОД 250 и 300=50

НОД 36и72=36

НОД 42и63=21

НОД 60и150=30

НОК 12 и 18=6

НОК 2 и 3=1

НОК 6 и 18=6

НОК 4 и 6=2

НОК 15 и 25=5

4,7(81 оценок)

Открыть все ответы

Ответ:

Ogurchick

11.01.2023

Пусть проводится 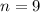n = 9 одинаковых испытаний, в каждом из которых то самое событие 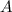— бракованная деталь — происходит с одинаковой вероятностью 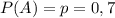P(A) = p = 0,7 и не происходит с одинаковой вероятностью 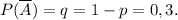$P(\overline{A}) = q = 1 - p = 0,3.$ Такую совокупность условий называют схемой Бернулли с параметрами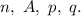 n, ~ A, ~ p, ~ q.

1) Если при проверке окажется ровно 5 качественных деталей, то будет 4 бракованных деталей;

Вероятность того, что в схеме Бернулли событие 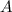произойдет ровно 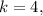k = 4, обозначают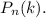 $P_{n}(k).$

Воспользуемся теоремой Бернулли: в схеме Бернулли с параметрами 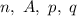n, ~ A, ~ p, ~ q справедливо равенство 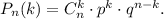$P_{n}(k) = C^{k}_{n} \cdot p^{k} \cdot q^{n-k}.$ Это равенство называют формулой Бернулли.

Имеем:

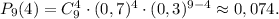
$P_{9}(4) = C^{4}_{9} \cdot (0,7)^{4} \cdot (0,3)^{9-4} \approx 0,074.$

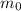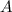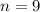2) Частота $m_{0}$ наступления события в n=9 независимых повторных испытаниях называется наивероятнейшим количеством (появления этого события), если ей соответствует наибольшая вероятность. Оно определяется по формуле:

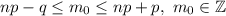
$np - q \leq m_{0} \leq np + p, ~ m_{0} \in \mathbb{Z}$

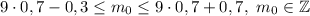
$9 \cdot 0,7 - 0,3 \leq m_{0} \leq 9 \cdot 0,7 + 0,7, ~ m_{0} \in \mathbb{Z}$

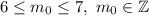
$6 \leq m_{0} \leq 7, ~ m_{0} \in \mathbb{Z}$

Таким образом, 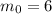$m_{0} = 6$ или $m_{0} = 7.$

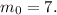
ответ: 1) 0,074; 2) 6 или 7.

4,5(73 оценок)

Ответ:

jykov2000

11.01.2023

х1=1;х2=2;х3=3

Пошаговое объяснение:

Матричный вид записи: Ax=b, где

А= $\left[\begin{array}{ccc}3&-1&0\\0&2&-1\\1&0&1\end{array}\right]$ b = 1;1;4 (Сверху вниз, в один столбец)Далее строим расширенную матрицу ( Также, только значения б добавляем справа под квадратную скобку)Обозначим через aij элементы i-ой строки и j-ого столбца. Первый этап. Прямой ход Гаусса. Исключим элементы 1-го столбца матрицы ниже элемента a1,1. Для этого сложим строку 3 со строкой 1, умноженной на -1/3: $\left[\begin{array}{ccc}3&-1&0\\0&2&-1\\0&1/3&1\end{array}\right]$ b = 1; 1; 11/3 (также сверху вниз, в один столбец)Исключим элементы 2-го столбца матрицы ниже элемента a2,2. Для этого сложим строку 3 со строкой 2, умноженной на -1/6: получим (буду писать текстом, так быстрей) 1 строка = 3;-1;0, 2 строка 0;2;-1, 3 строка 0;0;7/6. b = 1;1;7/2Делим каждую строку матрицы на соответствующий ведущий элемент, получаем: 1 строка = 1;-1/3;0, 2 строка = 0;1;-1/2, 3 строка = 0;0;1. b = 1/3;1/2/3Из расширенной матрицы восстановим систему линейных уравнений, Базисные переменные x1, x2, x3. и получаем: x1=1/3+1/3(х2);х2=1/2+1/2(х3);х3=3Подставив нижние выражения в верхние, получим решение: х1=1;х2=2;х3=3