а) (2 cos x + 1)( 2 sin x - √3) = 0
2 cos x + 1 = 0 или 2 sin x - √3 = 0
cos x = - 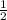 sin x =
sin x = 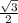
x = arccos(-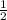 )+2Пn x =
)+2Пn x = 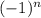 arcsin
arcsin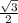 +Пn
+Пn
x = 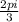 +2Пn x =
+2Пn x = 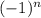 *
*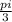 +Пn
+Пn
pi это П
б) 2 cos x - 3 sin x cos x = 0
cos x (2-3sinx) = 0
cos x = 0 или 2 - 3 sinx = 0
x = 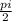 +2Пn sin x = -
+2Пn sin x = -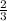
x = 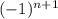 *arcsin
*arcsin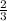 +Пn
+Пn
в) 4 sin²x - 3 sinx = 0
sin x (4sinx - 3) = 0
sin x = 0 или 4sinx - 3 = 0
x = 2Пn x =(-1)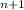 *arcsin
*arcsin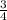 +Пn
+Пn
г)2 sin²x - 1 = 0
(√2sinx -1)(√2sinx+1) = 0
√2sinx-1 = 0 или √2sinx+1 = 0
sin x = √2/2 sin x = -√2/2
x = 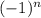 *
*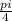 +Пn x =
+Пn x = 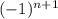 *
*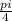 +Пn
+Пn
Пошаговое объяснение:
формула для оси симметрии х = - b/2a
расстояние между точками 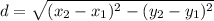
поскольку у нас точки пересечения с осью ОХ, они имеют координаты (х;0) и формула будет иметь вид d = х₂ - х₁
a) y=x² -4x +3
ось симметрии x = - (-4/2) = 2 x=2
точки пересечения с осью ОХ
x² -4x +3=0 ⇒ х₁= 1; х₂=3
точки (1;0) и (3;0)
расстояние между точками d = 3 - 1 = 2
b) y=x² + 2x -8
ось симметрии x = - (2/2) = 2 x= -1
точки пересечения с осью ОХ
x² + 2x -8=0 ⇒ х₁= -4; х₂=2
точки (-4;0) и (2;0)
расстояние между точками d = 2 - (-4) = 6
c) y=x² -4x -5
ось симметрии x = - (-4/2) = 2 x=2
точки пересечения с осью ОХ
x² -4x -5 =0 ⇒ х₁= -1; х₂= 5
точки (-1;0) и (5;0)
расстояние между точками d = 5 - (-1) = 6
d) y= -2x² + 4x + 6
ось симметрии x = - (4/4) = 1 x=1
точки пересечения с осью ОХ
x² -4x -5 =0 ⇒ х₁= -3; х₂= 3
точки (-1;0) и (3;0)
расстояние между точками d = 3 - (-1) = 4
36/х+3=36/(х-2)
получаем квадратное уравнение
х 2-2х-24=0
х=6, было сначала 6 коробок и положили по 6 карандашей
ответ: 6.