a-15 b-23 :2получиться нужное нам число складываем и получаем 38 делаем его на 2 и получаем 19.
эйлер родился 15 апреля 1707 г., в Швейцарии. Его отец, Пауль Эйлер, был пастором Реформатской церкви. У Леонарда было две младшие сестры – Анна Мария и Мария Магдалена. Вскоре после рождения сына, семья переезжает в городок Риен. В тринадцать лет Эйлер-младший поступает в Базельский университет, и в 1723 г. получает степень магистра философии. Открыл множества открытий среди них была Теория чисел он доказал малую теорему Ньютона а так же внёс ценные дополнения в теорию совершенных чисел, над которой с увлечением трудился не один математик.
Иване Матеевиче Виноградове- родился 2 сентября 1891 года в селе Милолюб. Среднее образование получил в реальном училище. В 1910 году поступил на физико-математический факультет Петербургского университета.Работы Виноградова по преимуществу посвящены аналитической теории чисел. Он решил ряд проблем, которые считались недоступными математике начала XX века. В числе прочего создал один из самых сильных и общих методов аналитической теории чисел — метод тригонометрических сумм. За разработанный метод был удостоен Сталинской премии I степени (1941).
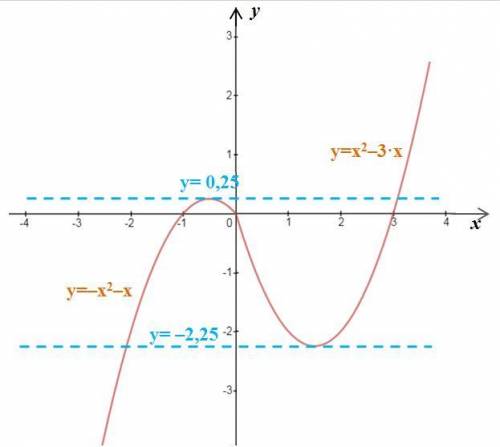
m= 0,25 и m = –2,25
Пошаговое объяснение:
Дана функция y=|x|·x–|x|–2·x.
1) x<0. Тогда левый кусок функции имеет вид:
y=|x|·x–|x|–2·x=–x·x–(–x)–2·x=–x²+x–2·x=–x²–x – это парабола, у которой ветви направлены вниз и с вершиной в точке
x= –(–1)/(2·(–1))= –0,5. Значение в вершине:
y(–0,5)= –(–0,5)²–(–0,5)=0,25.
Чтобы построит график определим значение функции в точке x=–1 и x=–2:
y(–1)= –(–1)²–(–1)=0; y(–2)= –(–2)²–(–2)=–2.
2) x≥0. Тогда правый кусок функции имеет вид:
y=|x|·x–|x|–2·x=x·x–x–2·x=x²–3·x – это парабола, у которой ветви направлены вверх и с вершиной в точке
x= –(–3)/(2·1)= 1,5. Значение в вершине:
y(1,5)= 1,5²–3·1,5= –2,25.
Чтобы построит график определим значение функции в точке x=0 и x=3:
y(0)= 0²–3·0=0; y(3)= 3²–3·3=0.
3) Построим график функций (см. рисунок). Тогда ответом будут только: m= 0,25 и m = –2,25, то есть только прямые y= 0,25 и y= –2,25 имеют с графиком ровно две общие точки.
При –2,25<m<0,25 прямые y=m имеют с графиком ровно три общие точки, а при m<–2,25 или 0,25<m прямые y=m имеют с графиком ровно одну общую точку.
при а = 15
при b = 23
(15+23)÷2=38÷2=19 (марок) - досталось каждому из ребят.
Голубая Даль ©