Пусть Настя смогла это сделать. Разделим числа на две группы -- те, которые делятся на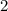 
, но не делятся на 
, и те, что делятся на . Заметим, что в обеих группах поровну чисел, а потому они должны чередоваться на окружности. Поделим все числа на 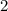-- получатся числа 
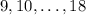. Теперь рядом стоящие числа взаимно просты, а четные и нечетные чередуются. Тогда рядом с числом 
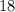должны располагаться два числа из 
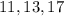(оставшиеся два нечетных делятся на 
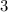), рядом с 
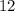тоже должны располагаться два из этих числа. Теперь можно попробовать расставить числа. Оказывается это возможно. Остается все умножить обратно на 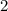и записать результат: 
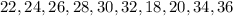(крайние тоже соседи).
1).х+ 5/25 + 17/25 = 1;
x+22/25=1
x=1-22/25
x=3/25
2).1 - х = 17/25 - 5/25;
-x=17/25-5/25-25/25
x=-(-13/25)
x=13/25
3).1 - х = 17/25 + 5/25;
-x=17/25+5/25-25/25
x=-(-3/25)
x= 3/25