Пошаговое объяснение:
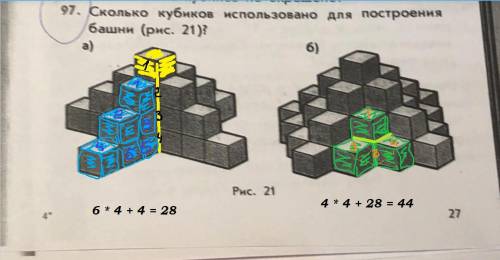
а) В данной фигуре под верхним кубиком лежат еще 3. Эти 4 кубика - ось фигуры. К ней в виде креста подходят 4 одинаковых ребра, каждое из которых состоит из 6 кубиков. Их легко сосчитать: они хорошо видны.
Всего: 6 * 4 + 4 = 24 + 4 = 28 (куб.)
ответ: 28
б) данная фигура отличается от первой тем, что между ребрами размещено еще 4 кубика: один вверху, три внизу.
Всего: 4 * 4 + 28 = 16 + 28 = 44 (куб.)
ответ: 44
Можно, конечно, считать слоями, нумеруя каждый, но деление на фрагменты удобнее
Пошаговое объяснение:
1) область определения функции: x ∈ R
2) проверим на четность:
y(-x) = -2x/(1 + x²) = -y(x) - функция нечетная
3) функция не периодическая
4) y = 0 только при х = 0, значит, точка пересечения с осями только (0; 0)
5) функция непрерывна
6) y' = (2(1 + x²) - 4x²)/(1+x²)² = (2 - 2x²)/(1 + x²)² = 0
2 - 2x² = 0
2x² = 2
x = -1 или x = 1
y'' = (4x³ - 12x)/(1+x²)³
y''(-1) > 0
y''(1) < 0
x = -1 - точка минимума
x = 1 - точка максимума
7) находим асимптоты:
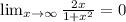
x = 0 - асимптота
найдем наклонные асимптоты:
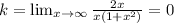
больше нет асимптот
2)853×9+(547061-159998):9=7677+387063=394740
3)636000:8-285000:6=79500-47500=32000
4)(748×9-1007×2)×8:4=(6732-2014)×8:4=4718×8:4=37744:4=9436