6×2=12 3×6=18 4×6=24
2×6=12 6×3=18 6×4=24
3×4=12 2×9=18 3×8=24
4×3=12 9×2=18 8×3=24
12×1=12 1×18=18 1×24=24
1×12=12 18×1=18 24×1=24
Пошаговое объяснение:
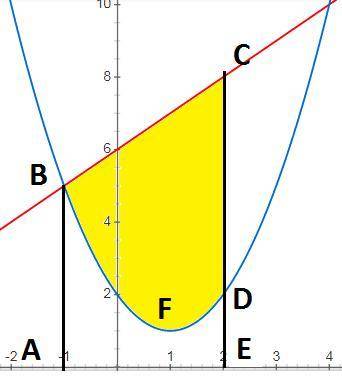
найдем точки пересечения графиков
y=x²-2x+2
y=x+6
x²-2x+2=x+6
x²-3x-4=0
x₁₋₂=(3±√(9+16)/2=(3±√25)/2=(3±5)/2={-1;4}
y=x+6 ;
AB=y(-1)=-1+6=5
EC=y(2)=2+6=8
AE=2-(-1)=3
Площадь фигуры ограниченной графиками
S=Sтрапеции ABCE - Sкриволинейной трапецииABFDE
Sтрапеции ABCE=(a+b)h/2=(AB+EC)*AE/2=(5+8)*3/2=13*3/2=19.5
Sкриволинейной трапецииABFDE=
2
=∫(x²-2x+2)dx=
-1
2
=((x³/3)-x²+2x) = (8/3)-4+4-((-1/3)-1-2)= (8/3)+(1/3)+3=(9/3)+3=6
-1
S=Sтрапеции ABCE - Sкриволинейной трапецииABFDE=19.5-6=13.5 (кв.ед)
18=9 и 2, 2 и 9, 6 и 3, 3 и 6, 18 и 1, 1 и 18
24=6 и 4, 4 и 6, 8 и 3, 3 и 8, 12 и 2, 2 и 12, 24 и 1, 1 и 240