Сделаем замену y'=z(x), получим уравнение z'=z+x.
Выполним еще одну замену: z(x)=u(x)*v(x), вычислим
+
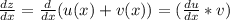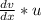
(du/dx)*v+u(dv/dx-v)=x (1) - таким стало уравнение после соответствующих подстановок.
Теперь выбираем функцию v(x), так чтобы v'-v=0, чтобы обнулить слагаемое
u(dv/dx-v) в уравнении (1). Решив это уравнение, оно элементарное с разделяющимися переменными, получим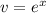 
Подставляем вычисленное v(x) в уравнение (1) и получаем:
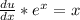, решаем его методом разделения переменных и получаем 
u(x)=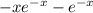
+C, где C-константа.
Возвращаемся к выражению z(x)=u(x)v(x)=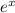
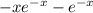*( +C )=-x-1+C*e^x.
Т.е.
y'(x)=-x-1+C*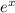 
.
Решаем это уравнение получаем dy=( -x-1+C* 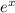)dx
Получаем y(x)=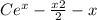
+C1, где С и С1 это константы которые находятся из начальных условий.
ответ: y(x)=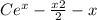 +C1, где С и С1- const
ответ: 1) (х-4) в кв. = х в кв. минус 4 в кв. умножить на 2 умножить на 4х плюс 4 в кв...ДАЛЕЕ ВСЕ ВОЗВОДИМ...= х в кв. минус 8х плюс 16.ВСЕ
2) (5-х) в кв. = 5 в кв. минус 2 умножить на 5х плюс х в кв...ВОЗВОДИМ...= 25 минус 10х плюс х в кв...ВСЕ
3) (3х-2) в кв. = (3х) в кв. минус 2 умножить на 3х и умножить на 2 плюс 2 в кв...ВОЗВОДИМ...= 9х в кв. минус 12х плюс 4. ВСЕ
4) (5m + 3n) в кв = 5m в кв. плюс 2 умножить на 5m и умножить на 3n плюс 3n в кв...ВОЗВОДИМ...= 25m в кв. плюс 30mn плюс 9n в кв.ВСЕ
СОРИ ДАЛЬШЕ ЛЕНЬ
если что в кв это типа в квадрате))
4+4+4=12
12÷6=2
4 в кубе это 64
64+64+64=192
192÷6=32