Для того чтобы решить уравнение (неравенство) с модулем, надо рассмотреть все промежутки на которых при раскрытии модуля подмодульное выражение меняет знаки
В нашем уравнении два модуля.
Воспользуемся раскрытием модуля методом "коридора"
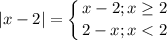
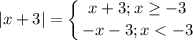
тогда рисуем "коридор"
__(2-x)__-3 ___(2-x)__ 2 __(x-2)______
(-x-3) (x+3) (x+3)
теперь 1 промежуток x< -3
2-x+(-x-3)=14
2-x-x-3=14
-2x-1=14
-2x= 15
x= -15/2
x= - 7.5
т.к. -7.5 < -3 то корень подходит
теперь 2 промежуток -3 ≤x<2
2-x+x+3=14
5=14
на этом промежутке решений нет
теперь 3 промежуток x≥2
x-2+x+3=14
2x+1=14
2x=13
x=6.5
т.к. 6,5 >2 то корень подходит
ответ: -7,5 и 6.5
Если диагональ квадрата равна 20, то сторона квадрата: a = 20/√2 = 10√2.
Найдём диаметр цилиндра: d = 8•2 = 16.
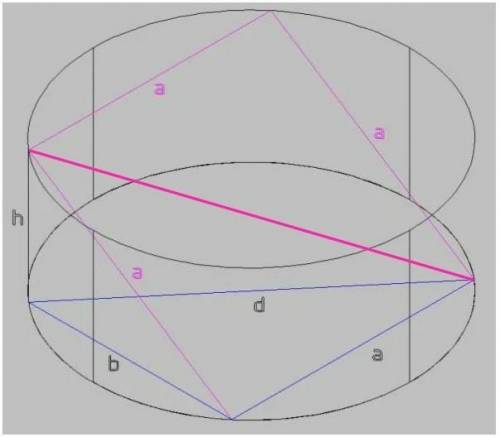
По условию плоскость квадрата АВСD не параллельна оси цилиндра. В этом случае центр квадрата совпадает с центром цилиндра.
На рисунке проекция квадрата на основание показана синим цветом.
b — проекция наклонной стороны квадрата на плоскость основания.
По теореме Пифагора: a² + b² = d² ;
b² = d² - a² = 16² - (10√2)² = 256 - 100•2 = 56;
b = √56 = 2√14.
И снова по теореме Пифагора, но уже для вертикально расположенного прямоугольного треугольника:
h² + b² = a² ;
h² = a² - b² = (10√2)² - (2√14)² = 200 - 56 = 144;
h = √144 = 12.
х+х-13+х+65=244. 3х=244-52. 3х=192. х=192:3. х=64 длина первого отрезка 64см