Данная система — пример системы линейных неравенств с одним неизвестным. Решением системы неравенств с одним неизвестным называется то значение неизвестного, при котором все неравенства системы обращаются в верные числовые неравенства. Решить систему неравенств — это значит найти все решения этой системы или установить, что их нет. Неравенства \( x \geq -2 \) и \( x \leq 3 \) можно записать в виде двойного неравенства: \( -2 \leq x \leq 3 \). ... Решать линейные неравенства с одним неизвестным вы уже научились. Знаете, что такое система неравенств и решение системы. Поэтому процесс решения систем неравенств с одним неизвестным не вызовет у вас затруднений
Пошаговое объяснение:
Пошаговое объяснение:
Метод математической индукции состоит из 2ух шагов.
1)Утверждение P(n) справедливо при n=1. (База индукции)
2)Для ∀k∈N из справедливости P(k) следует справедливость P(k+1)(индуктивный переход)
[a]
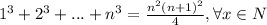
1 шаг: база индукции
Проверяем справедливость при n=1
1³+2³+...+n³=1
(1/4)*1²*(1+1)²=(1/4)*4=1
Верно
2 шаг: Индуктивный переход
Допустим равенство верно для n=k:
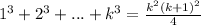
Докажем что формула равна и для n=k+1
(на месте k в формуле должно оказаться k+1)

Доказано
[b]

1 шаг: база индукции
Проверяем справедливость при n=1
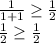
Верно
2 шаг: Индуктивный переход
Допустим равенство верно для n=k:
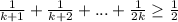
Докажем что формула равна и для n=k+1:


Выражение без скобок ≥1/2, выражение в скобках >0, значит выражение выполняется для k+1
Доказано
ищем прирост и делим на старую цену.
350-250=100
100*100% / 250 =40%