![t^2 - 8 t + [7-a] = 0 ,](/tpl/images/0495/7941/4dac0.png) где под
где под 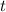 подразумевается квадрат переменной
подразумевается квадрат переменной 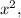 т.е.
т.е.  а его корнями
а его корнями 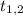 – квадраты искомых корней, если они различны, или его чётным корнем
– квадраты искомых корней, если они различны, или его чётным корнем 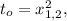 если корень биквадратного трёхчлена
если корень биквадратного трёхчлена 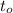 – единственный.
– единственный.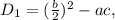 тогда
тогда ![D_1 = 4^2 - [7-a] = 9 + a .](/tpl/images/0495/7941/d229f.png) Потребуем, чтобы
Потребуем, чтобы 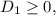 откуда следует, что
откуда следует, что 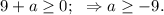
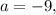 а корень биквадратного трёхчлена станет чётным
а корень биквадратного трёхчлена станет чётным  давая два искомых корня
давая два искомых корня 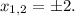 Это значение
Это значение 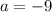 как раз уже и есть одно из искомых решений для параметра
как раз уже и есть одно из искомых решений для параметра 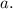
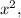 всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней
всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней 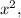 по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно
по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно 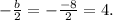 Отсюда следует, что правый квадрат искомых корней
Отсюда следует, что правый квадрат искомых корней 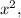 – всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.
– всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.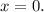 А значит, значение всего трёхчлена
А значит, значение всего трёхчлена ![x^4 - 8 x^2 + [7-a]](/tpl/images/0495/7941/7bbf9.png) взятое от
взятое от 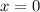 должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.
должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.![0^4 - 8 \cdot 0^2 + [7-a] < 0](/tpl/images/0495/7941/13440.png) ;
; ;
;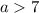 ;
;
Сумма всех трехзначных чисел равна
[(100+999)/2]×900=494550
Обозначим искомые числа a и b.
Тогда по условию
(494550-a-b)/600=a
Упростим выражение
494550-a-b=600a откуда
494550-b=601a
Для выполнения этого условия необходимо, чтобы 494550-b было кратно
601
Разделим 494550 на 601
Целая часть результата 822
Умножим 822 на 601
Получим 494022
На долю b остаётся 494550-494022=528
Таким образом, два искомых числа
822 и 528
Сделаем проверку
494550-822-528=493200
493200:822=600