а) Есть теорема: a/b < (a+1)/(b+1) при любых a > 0; b > 0; b > a
Для доказательства найдем разность через общий знаменатель:
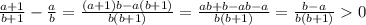
Конечная дробь больше 0, потому что числитель больше 0 (потому что b > a) и знаменатель тоже больше 0.
Если разность дробей больше 0, то первая дробь больше второй.
10/11 > 9/10 > 8/9.
Наибольшее 10/11.
б) 11/20 = 22/40 > 21/40
11/20 = 33/60 > 31/60.
Наибольшее 11/20
в) 23/48 = 24/48 - 1/48 = 1/2 - 1/48,
17/36 = 18/36 - 1/36 = 1/2 - 1/36
35/72 = 36/72 - 1/72 = 1/2 - 1/72.
Чем больше знаменатель, тем меньше дробь. 1/72 < 1/48 < 1/36
Чем меньше вычитают из числа 1/2, тем больше остается.
1/2 - 1/72 > 1/2 - 1/48 > 1/2 - 1/36
Наибольшее 35/72
а) Есть теорема: a/b < (a+1)/(b+1) при любых a > 0; b > 0; b > a
Для доказательства найдем разность через общий знаменатель:
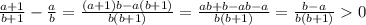
Конечная дробь больше 0, потому что числитель больше 0 (потому что b > a) и знаменатель тоже больше 0.
Если разность дробей больше 0, то первая дробь больше второй.
10/11 > 9/10 > 8/9.
Наибольшее 10/11.
б) 11/20 = 22/40 > 21/40
11/20 = 33/60 > 31/60.
Наибольшее 11/20
в) 23/48 = 24/48 - 1/48 = 1/2 - 1/48,
17/36 = 18/36 - 1/36 = 1/2 - 1/36
35/72 = 36/72 - 1/72 = 1/2 - 1/72.
Чем больше знаменатель, тем меньше дробь. 1/72 < 1/48 < 1/36
Чем меньше вычитают из числа 1/2, тем больше остается.
1/2 - 1/72 > 1/2 - 1/48 > 1/2 - 1/36
Наибольшее 35/72
f=7x+8y-xy-z=0
f1`(x-x0)+f2`(y-y0)+f3`(z-z0)=0
f1`=df/dx=7-y; f2`=df/dy=8-x; f3`=df/dz=-1
(7-y)(x-1)+(8-x)(y-1)+(-1)(z-14)=0-уравнение касательной пл-ти
7x-7-xy+y+8y-8+xy+x-z+14=0
8x+9y-z-1=0