Задание 1.
0,(7) = 7/9;
0,8(5) = 77/90;
0,73(4) = 661/900;
8,342(3) = 8 1027/3000 .
Задание 2.
5/6 = 0,8(3);
9/11 = 0,(81).
Пошаговое объяснение:
Задание 1.
Периодическую дробь обратите в обыкновенную: 0, (7) ; 0,8(5); 0, 73(4); 8,342(3)
0,(7)
1) Количество цифр в периоде = 1.
2) Количество цифр после запятой, но до периода = 0.
3) Число из цифр после запятой, включая период, = 7.
4) Число после запятой, но до периода = 0.
5) Числитель искомой дроби = п. 3 - п. 4 = 7 - 0 = 7.
6) Знаменатель искомой дроби - число, которое составлено из такого количества девяток, которое указано в п. 1, и из такого количества нулей, которое указано в п. 2 = 9 .
ответ: 0, (7) = 7/9 .
0,8 (5)
1) Количество цифр в периоде = 1.
2) Количество цифр после запятой, но до периода = 1.
3) Число из цифр после запятой, включая период, = 85.
4) Число после запятой, но до периода = 8.
5) Числитель искомой дроби = п. 3 - п. 4 = 85 - 8 = 77.
6) Знаменатель искомой дроби - число, которое составлено из такого количества девяток, которое указано в п. 1, и из такого количества нулей, которое указано в п. 2 = 90.
ответ: 0,8(5) = 77/90 .
0,73(4)
1) Количество цифр в периоде = 1.
2) Количество цифр после запятой, но до периода = 2.
3) Число из цифр после запятой, включая период, = 734.
4) Число после запятой, но до периода = 73.
5) Числитель искомой дроби = п. 3 - п. 4 = 734-73=661.
6) Знаменатель искомой дроби - число, которое составлено из такого количества девяток, которое указано в п. 1, и из такого количества нулей, которое указано в п. 2 = 900.
ответ: 0,73(4) = 661/900 .
8,342(3)
1) Количество цифр в периоде = 1.
2) Количество цифр после запятой, но до периода = 3.
3) Число из цифр после запятой, включая период, = 3423.
4) Число после запятой, но до периода = 342.
5) Числитель искомой дроби = п. 3 - п. 4 = 3423-342=3081.
6) Знаменатель искомой дроби - число, которое составлено из такого количества девяток, которое указано в п. 1, и из такого количества нулей, которое указано в п. 2 = 9000.
7) Дробную часть сокращаем на 3:
3081 / 9000 = 1027/3000.
ответ: 8,342(3) = 8 1027/3000 .
Задание 2.
Обыкновенную дробь представьте в виде периодической дроби :
5/6, 9/11.
Делим числитель на знаменатель и заключаем в скобки периодическую часть. В первом случае период равен (3) , во втором случае (81).
5/6 = 0,833333... = 0,8(3)
9/11 = 0,81818181... = 0,(81)
ответ: 5/6 = 0,8(3); 9/11 = 0,(81).
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
![\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/e1322.png)
Приведем к ступенчатому виду. Применяем операцию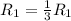 
к 
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию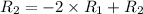 
к 
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию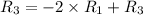 
к 
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/0d2b8.png)
Применяем операцию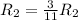 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/8a8f7.png)
Применяем операцию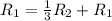 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/c212b.png)
Применяем операцию 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]](/tpl/images/1055/0577/960ac.png)
Применяем операцию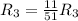 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/ffa18.png)
Применяем операцию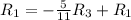 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/a5101.png)
Применяем операцию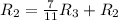 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]](/tpl/images/1055/0577/927aa.png)
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
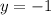
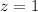
Решением является множество упорядоченных пар, которые удовлетворяют системе.
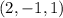
Да, правильний ответ