-6
Пошаговое объяснение:
Дано: x=2n+8 y=3n+6
Найти: Наименьшее произведение х и у.
Составим функцию f(n)=xy
f(n)=(2n+8)(3n+6)=6n²+24n+12n+48=6n²+36n+48 парабола, ветви которой направлены вверх, т.к. коэффициент а=6>0. Значит, наименьшее значение данная функция (парабола) принимает в точке, которая является её вершиной. Найдём вершину параболы:
х(в)=-b/2a = -36/(2*6)=-36/12=-3
y(в) = (2(-3)+8)(3*(-3)+6)=(-6+8)(-9+6)=2*(-3)= -6
у= -6 - наименьшее значение данной функции, т.е. наименьшее значение произведения х и у.
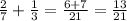часть всей работы,
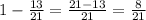часть всей работы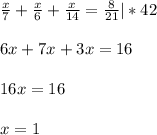
Чтобы найти дробь от числа, надо число умножить на эту дробь. Умножаем их по правилу умножения числа на дробь: числитель умножаем на число, а знаменатель оставляем без изменения.
Чтобы найти число по его дроби, это число делим на эту дробь. Чтобы разделить число на дробь, надо данное число умножить на число, обратное к дроби (то есть на перевернутую дробь). Чтобы умножить дробь на число, надо числитель умножить на это число, а знаменатель оставить без изменения.
Задача.
1) 120× 2/5=48(мест)- занято;
2) 120-48=72(мест) - свободно
ответ:72 места.