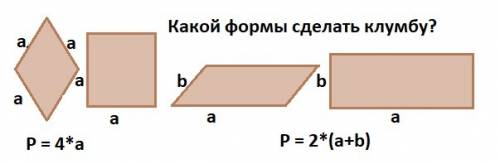
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
Находим точку пересечения сторон, решив систему уравнений.
1) 8x + 3y = -1
2) 2x + y = 1
Применяем метод Гаусса.
3) 8*x + 4*y = 4 - умножили на 4 ур. 2)
4) y = 5, x = - 2 - точка А(-2;5)
Также пересечение с диагональю.
5) 8x + 3y = -1
6) 3x + 2y = - 3
7) 24x + 9y = -3
8) 24x +16y = - 24
9) - 7*y = 21
10) y = -3, x = 1. Точка В(1;-3)
И так же для третьей точки пересечения.
11) 2x + y = 1
12) 3x + 2y = -3
13) x = 5, y = -9. Точка С(5;-9)
Решение не закончено. Рисунок к задаче в приложении.