Центр окружности расположен на координатной прямой в точке в (1),а точка а (—3) левый конец ее диаметра. единичный отрезок равен 1см. найдите длину окружности.
Для начала округлим число х до трех значащих цифр, то есть, до числа х1.
1) Число 11,445:
В данном случае, трех значащих цифр будет достаточно, поэтому число х1 примет значение 11,4.
2) Число 20,43:
Также, трех значащих цифр будет достаточно, поэтому число х1 примет значение 20,4.
3) Число 1,2376:
Тут у нас уже округление до трех значащих цифр будет недостаточно, поэтому нам придется округлить число х1 до четырех значащих цифр. В результате, число х1 примет значение 1,238.
Теперь, нам нужно вычислить границы абсолютной и относительной погрешностей для каждого числа х1.
Для этого, мы будем использовать следующие формулы:
Таким образом, для числа 11,445:
- Абсолютная погрешность равна 0,045,
количество верных цифр после округления - 3.
- Относительная погрешность равна 0,39%,
количество верных цифр после округления - 3.
Для числа 20,43:
- Абсолютная погрешность равна 0,03,
количество верных цифр после округления - 3.
- Относительная погрешность равна 0,15%,
количество верных цифр после округления - 3.
Для числа 1,2376:
- Абсолютная погрешность равна 0,0004,
количество верных цифр после округления - 4.
- Относительная погрешность равна 0,032%,
количество верных цифр после округления - 4.
Надеюсь, я смог помочь вам понять эту задачу! Если у вас возникнут еще вопросы, пожалуйста, спрашивайте.
Для решения данной задачи, давайте вначале посмотрим на каждое из выражений по отдельности.
1) re(sh(z+1)cos(y+1)sh(x))
Функция re() возвращает действительную часть комплексного числа, поэтому выражение в скобках должно быть комплексным числом. Для этого используем формулу Эйлера:
sh(z) = (exp(z) - exp(-z))/2i
Таким образом, мы можем раскрыть первое выражение:
точка с координатой 1 - центр окружности, -3 - левый конец диаметра. Из этого можно найти длину радиуса окружности:
Длина окружности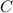
вычисляется по формуле: 
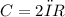, отсюда 
.
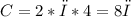ответ: 8π