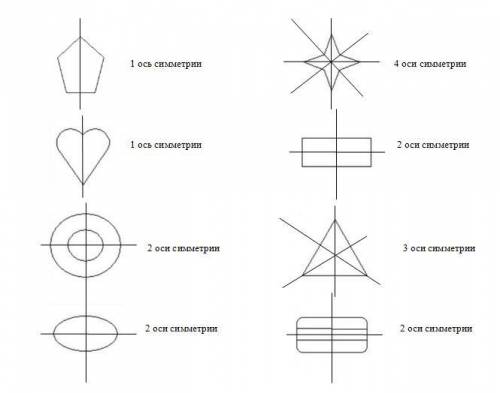
Сначала определимся с количеством осей симметрии каждой фигуры. См. рис.1 и 2. (предполагается, что третья фигура в верхнем ряду - это 2 окружности, хотя, больше это похоже на 2 эллипса. Но, если принять второе, то количество фигур, имеющих 2 оси симметрии становится равным 5, и выполнить условие задачи не представляется возможным).
Теперь перемещаем фигуры, согласно условию. (Рис.3)
По диагонали располагаем фигуры с двумя осями симметрии.
По второй диагонали - фигуры с одной осью симметрии.
Затем размещаем фигуры с четырьмя осями симметрии.
Ну и оставшиеся раскидываем по оставшимся четырем клеткам.
Думаю, задача записана не совсем верно. Объём воды при замерзании не может увеличиться в 8 дм3. Видимо, следует читать на 8 дм3. И в вопросе тоже неточности. Видимо, следует читать На сколько увеличится объём.
22*4=88 (л) - объём воды в 22 вёдрах 1л воды = 1 дм3
88+8=96 (дм3) - объём льда
Составляем пропорцию:
из 88 л - 96 дм3
из 11 л - х дм3
Т.к. пропорциональность прямая, то х=11*96/88=12 (дм3)
Объём 11л воды увеличится на 12-11=1 (дм3)
S=a^2, S - площадь, a - сторона.
Площадь известна, найдем сторону:
196=a^2
a=14(берем только положительное значение a)
Радиус окружности, описанной около квадрата, равен половине диагонали квадрата.
r=d/2, где r - радиус, d - диагональ квадрата.
Диагональ квадрата найдем по теореме Пифагора:
стороны квадрата - катеты, диагональ - гипотенуза.
d^2=a^2+a^2
d^2=2a^2
d=a√2
Тогда радиус:
r=a√2/2
Находим площадь круга:
S=пr^2=п*a^2/2
Подставляем значения:
S=п*14^2/2=98п
ответ: 98п