1) 
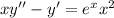
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на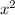 
, получаем
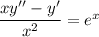
В левой части уравнения это ни что иное как формула производной частного, то есть :
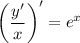
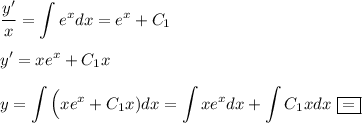
Подсчитаем отдельный интеграл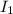 
по частям.
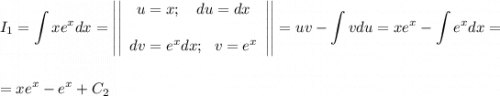
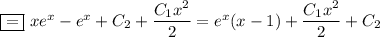
2) 
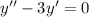
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена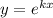 
, перейдём к характеристическому уравнению: 
, 
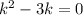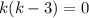корни которого 
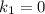и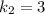 
. Тогда общее решение диф. уравнения: 
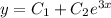и его первая производная 
.
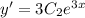Осталось найти константы C₁ и C₂ , подставляя начальные условия.
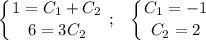
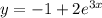— частное решение.
Поскольку при выкладывании по 8 и по 9 плиток в ряд прямоугольников не получается, а остаются неполные ряды, то количество плиток делится на 8 и на 9 с остатками.
Остаток от деления любого числа на 8 не может быть больше 7. По условию это число на 6 больше, чем остаток от деления на 9. Но остаток от деления на 9 тоже не равен нулю. Значит, остаток от деления на 8 может быть равен только 7. А остаток от деления на 9 равен 1.
Общее количество плиток меньше 100, иначе их хватило бы на квадратную площадку со стороной в 10 плиток. Среди чисел меньше 100 надо найти такое, которое делится на 8 с остатком 7 и на 9 с остатком 1. Проверив все числа в пределах 100, делящиеся на 9 с остатком 1, получим ответ: 55 плиток.
Пошаговое объяснение:
≈ 62,5 см²
Пошаговое объяснение:
Пусть S - площадь закрашенной фигуры.
S = S круга - S квадрата.
S круга = πR².
D = 10 см.
R = D : 2 = 10 : 2 = 5 см
S круга = πR² = π(5)²=25π см²
S квадрата = a², где a - сторона квадрата.
P = 16 см.
a = P : 4 = 16 : 4 = 4 см.
S квадрата = 4² = 16 см²
S = 25π - 16 ≈ 62,5 см²