Дано: y = 2/3*x³ + x + 2/3.
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
x1 ≈ -0.5535 - нуль функции.
3. Интервалы знакопостоянства.
Y<0 - X∈(-∞;-0.55], Y>0 - X∈[-0.55;+∞)
4. Пересечение с осью OY. Y(0) = 2/3 = 0,(6)
5. Исследование на чётность.
Важно: у четных -только чётные степени, у нечётных - только нечётные.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
6. Первая производная. Y'(x) = 2*x² +1 = 0 , х² = - 0,5.
Корней нет.
7. Локальные экстремумы - нет.
8. Интервалы возрастания и убывания.
Возрастает во всем интервале определения.
9. Вторая производная - Y"(x) = 4* x = 0
Корень производной - точка перегиба Х₆=0
10. Выпуклая “горка» Х∈(-∞; Х₆=0]
Вогнутая – «ложка» Х∈[Х₆=0; +∞).
11. График в приложении.
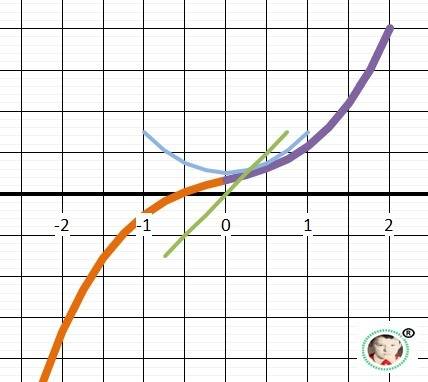
-100 -99 -94 0 96 98 99
Для решения задачи стоит понимать: самые простое решение - если одно из чисел равно 0. Тогда их произведение равно 0.
Далее мы ищем оставшиеся числа: их сумма соответственно должна быть равна 0. Самый простой пример: три пары различных целых чисел. В каждой паре одинаковые по модулю различные целые числа, не равные 0. Например: -1 и 1; -2 и 2; -3 и 3.
Тогда простейшим примером будет:
-3 -2 -1 0 1 2 3 (сумма всех чисел равна их произведению (нулю)
Для примера в начале задания использовался другой алгоритм, но результат также верный.