Приведение к стандартному виду:
\begin{gathered}\displaystyle 2,\!1 \cdot a^2 b^2 c^4 \cdot \bigg ( - 1\frac{3}{7} \bigg ) \cdot bc^3 d = - \bigg ( \frac{21}{10} \cdot \frac{10}{7} \bigg ) \cdot a^2 \cdot b^2b \cdot c^4c^3 \cdot d = = - \frac{21}{7} \cdot a^2 \cdot b^{2+1} \cdot c^{4+3} \cdot d = \boxed {- 3a^2 b^3c ^7d}\end{gathered}2,1⋅a2b2c4⋅(−173)⋅bc3d=−(1021⋅710)⋅a2⋅b2b⋅c4c3⋅d==−721⋅a2⋅b2+1⋅c4+3⋅d=−3a2b3c7d
Коэффициент одночлена: \boxed {-3}−3 .
Задание 2.
Формула для нахождения объема прямоугольного параллелепипеда (VV - объем; xx , yy , zz - измерения прямоугольного параллелепипеда): V=xyzV=xyz .
Значит, объем исходного параллелепипеда равен:
\begin{gathered}V = \Big (4a^2b^5 \Big ) \cdot \Big (3ab^2 \Big ) \cdot \Big (2ab \Big ) = \Big (4 \cdot 3 \cdot 2 \Big ) \cdot a^2aa \cdot b^5b^2b = = 24 \cdot a^{2+1+1} \cdot b^{5+2+1} =\boxed {24a^4b^8}\end{gathered}V=(4a2b5)⋅(3ab2)⋅(2ab)=(4⋅3⋅2)⋅a2aa⋅b5b2b==24⋅a2+1+1⋅b5+2+1=24a4b8
Задание 1.
Натуральное значит больше нуля и целое.
Значит ищем целое число кратное 11,кратное 3 и некратное9, число двузначное значит меньше 100
Таких числе будет два 33 и 66
Задание 2

Задание 3 не полностью
Задание 4 не полностью
Задание 5
300л =3,3 см
500л=? Обозначим х
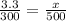
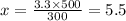
5,5 см
Задание 6
90:6=15
Могут, т. к. 90 делится на 6 без остатка.
Задание 7.
220*0,15=33
33 жеребёнка
Задание 8.
(2103 − 1328) : 31 + 5 · 204:15=
=775:31+204:3=25+68=93
Задание 9
Зелёный 250 г 220 руб.
Цена за кг220*4=880 руб, 4 пачки
Зелёный с жасмином 200 г 180 руб.
Цена за кг 180*5=900 руб, 5 пачек
Чёрный с бергамотом 250 г 230 руб.
Цена за кг230*4=920 руб, 4 пачки
Чёрный 100 г 91 руб.
Цена за кг 91*10=910 руб, 10 пачек
Дешевле всего за кг зеленый 880 рублей
Задание 10,11 - нет рисунков
решение: 7:28=
сокращаем= 1:4
2) ответ: 22800000 см= 280км
3)7/21