ответ:
(24+х)-21=10. (24+х)-21=10
24+х=21+10. 24-21+х=10
24+х=31. 3+х=10
х=31-24. х=10-3
х=7. х=7
(24+7)-21=10. (24+7)-21=10
10=10. 10=10
(45-у)+18=58. (45-у)+18=58
45-у=58-18. 45+18-у=58
45-у=40. 53-у=58
у=45-40. у=58-53
у=5. у=5
(45-5)+18=58. (45-5)+18=58
58=58. 58=58
56-(х+12)=24. 56-(х+12)=24
х+12=56-24. 56-12+х=24
х+12=32. 44+х=24
х=32-12. х=44-24
х =20. х=20
56-(20+12)=24. 56-(20+12)=24
24=24. 24=24
55-(х-15)=30. 55-(х-15)=30
х-15=55-30. 55+15-х=30
х-15=25 70-х=30
х=25+15. х=70-30
х=40. х=40
55-(40-15)=30. 55-(40-15)=30
30=30. 30=30
ответ: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Пусть пуд сахара стоит х, а фунт чая - y. Тогда можем составить и решить такую систему уравнений:
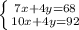
Решаем систему методом вычитания (находим x):
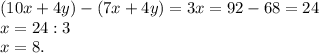
Теперь можно найти y:
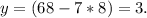
Итого: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Задачу можно решить и арифметически, заметив, что и там, и там по 4 фунта чаю:
1). 92 - 68 = 24 (рубля) - разница между 7 пулами и 10 пудами сахара.
2). 10 - 7 = 3 (пуда) - разница между 7 пудами и 10 пудами сахара.
3). 24 : 3 = 8 (рублей) - стоит пуд сахара.
4). (68 - 8 * 7) : 4 = 3 (рубля) - стоит фунт сахара.
Найдем точку T в которую опускается перпендикуляр из точки P на прямую проходящую через M1M2
Прямая:
M1M2=(-7,-21,-14)
x=-7t+5
y=-21t+4
z=-14t+6
Получили точку T(-7t+5;-21t+4;-14t+6)
Вектор TP=(2+7t-5; -5+21t-4; 7+14t-6)=(7t-3; 21t-9; 14t+1)
Если векторы перпендикулярны то их скалярное произведение равно 0:
(M1M2,TP)=-7*(7t-3)-21*(21t-9)-14*(14t+1)=0
7t-3+63t-27+28t+2=0
t=28/98=2/7
отсюда
T=(3; -2; 2)
TP=(-1; -3; 5)
Ну и отложим вектор -TP=(1; 3; -5) из точки T что бы получить симметричную точку
Q=(4; 1; -3)