Проверим это правило посчитав определитель второй степени:
![[\begin{array}{cc}1&2\\4&5\end{array}]\right] = 1*5 - 2*4 = -3](/tpl/images/0150/1870/c0c97.png)
Поменяем столбцы местами:
![[\begin{array}{cc}2&1\\5&4\end{array}]\right] = 2*4 - 1*5 = 3](/tpl/images/0150/1870/aa59c.png)
Если брать некоторые абстрактные значения:
![[\begin{array}{cc}a_1&a_2\\a_3&a_4\end{array}]\right]= a_1*a_4 - a_2*a_3](/tpl/images/0150/1870/72ec5.png)
Пусть 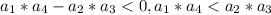
Поменяем столбцы местами:
![[\begin{array}{cc}a_2&a_1\\a_4&a_3\end{array}]\right] = a_2*a_3 - a_1*a_4 0](/tpl/images/0150/1870/45e70.png)
Далее можно было бы рассмотреть определитель n*n, но мне кажется, что и эта демонастрация будет весомым подкреплением моего заверения: что при перестановке столбцов знак определителя меняется на противоположный.
Во-первых, очень часто в системе уравнений вообще невозможно посчитать определитель, так как матрица отвечающая системе оказывается не квадратной.
А во-вторых, разумеется, определитель системы поменяет знак, если системе будет отвечать квадратная матрица и вы переставите столбцы.
Главное не путать матрицу элементов и определитель этой матрицы, это разные сущности!
Когда вы переставляете столбцы - вы меняете определитель, а система остается эквивалентной (когда перестановка осуществляется в пределах левой части, или в пределах правой. При переносе столбцов из левой в праву, или из правой в левую, надо домножать столбец на -1).
1м 45 с-100 %
105с-1 м 45с
1)105с÷100%=1,05с-1%
2)1,05×15=15,75с-быстрее Таня
3)105-15,75=89,25с-результат Тани
89,25с=1м 29,25с-или 1 минута 29с