a=1
Пошаговое объяснение:
Мы имеем 2 точки с координатами:
1) координаты вершины параболы (–1; 2) – отмечена красными стрелками
2) координаты второй точки (0; 3) – отмечено голубой стрелкой.
Подставим координаты каждой точки в формулу y=ах²+bx+c:
a×(–1)²+b×(–1)+c=2
a×0²+b×0+c=3
а–b+c=20+0+c=3a–b+c=2
c=3
Подставим значение с в уравнение
а–b+c=2
a–b+3=2
a–b=2–3
a–b= –1
Вершина параболы вычисляется по формуле:
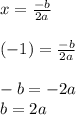
подставим значение b в уравнение:
а–b= –1
a–2a= –1
–a= –1
a=1
Теперь подставим значение а в уравнение:
b=2a=2×1=2
Итак: а=1, b=2, c=3, тогда уравнение будет иметь вид: y=х²+2b+3

1)12/21 что на двух кубиках в сумме четное
1/6 что на третьем выпадет 4
2)Вероятность того, что произойдут:
1 промах и 3 попадания равна 0.2 * 0.8 * 0.8 * 0.8
1 попадание, 1 промах и 2 попадания равна 0.8 * 0.2 * 0.8 * 0.8
2 попадания, 1 промах и 1 попадание равна 0.8 * 0.8 * 0.2 * 0.8
3 попадания и 1 промах равна 0.8 * 0.8 * 0.8 * 0.2
Полная вероятность 1 промаха и 3 попаданий в любом порядке, это:
0.2*0.8^3 + 0.8*0.2*0.8^2 + 0.8^2 * 0.2*0.8 + 0.8^3 * 0.2 =
4*0.2*0.8^3 = 4 (1/5)(4/5)^3 = (4/5)^4 = 256/625 = 0.4096 = 40.96 %
3)Представим себе таких параллельных вселенных, в каждой и которых есть точно такой же магазин. Тогда всего во всех этих магазинах пальто от первой фабрики и пальто от второй фабрики.
Мы считаем, что любое пальто покупатели могут взять – равновероятно. Т.е. можно считать, что всего во все эти магазины приходят покупателей и раскупают все эти пальто.
Всего из купленных пальто от первой фабрики будет баркованных.
Всего из купленных пальто от второй фабрики будет баркованных.
Полное число бракованных пальто от обеих фабрик во всех магазинах будет
А вообще во всех этих магазинах, как мы уже говорили выше, пальто от обеих фабрик.
ответ:3.545%