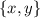такие, что 
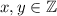и 
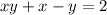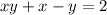. для 
.
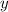к обеим частям уравнения:
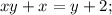
за скобки в левой части уравнения: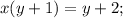
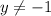, и разделим обе части уравнения на 
:
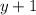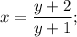
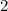в числителе в правой части уравнения как 
:
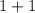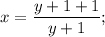
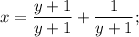
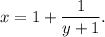
является целым тогда и только тогда, когда член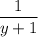 
в правой части уравнения является целым. 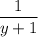является целым тогда и только тогда, когда знаменатель противоположен или является делителем числителя.
имеет ровно один делитель: . Получаем:
..
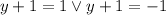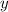к обеим частям уравнений: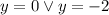
.:
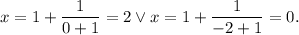
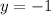, подставив в исходное уравнение :
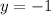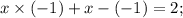
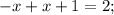
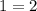, следовательно, при 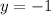решений нет.
