Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
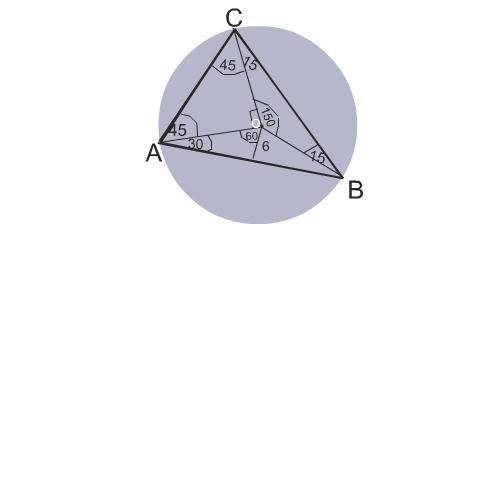
Радиусами окружности исходный треугольник АВС делится на 3 равнобедренных треугольника.
В трегольнике СОВ острые углы равны по 15 градусов, поэтому
угол СОВ равен 180-30=150 градусов.
Угол СОА равен 90 градусов по условию задачи.
Отсюда
угол АОВ равен 360 -90-150=120 градусов.
Расстояние от О до АВ равно 6 см.
Этот отрезок делит треугольник АОВ на два прямоугольных треугольника,острый угол ОАВ равен 30 градусов.
Радиус ОА в этом треугольнике является гипотенузой и вдвое больше катета, противолежащего углу 30 градусов.
Радиус окружности равен
6*2=12 см
биноминальное распределение - распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.
это распределение интенсивно используется в картах контроля качества, p - доля годной продукции, q - доля брака.
в телекоммуникации q - доля необслуженных (потерянных) вызовов.
представим себе испытание с двумя возможными : а и ас, где, скажем, а условно означает «успех», дополнительное событие ас – «неудачу».
серию независимых испытаний такого рода с одной и той же вероятностью успеха р=р(а) называют испытаниями бернулли.
примером может служить последовательное бросание монеты, в котором условно выпадение герба есть успех, а выпадение решетки – неудача.
каждый исход n испытаний здесь можно описать цепочкой событий , где или ас соответственно означает успех или неудачу в k-м испытании,