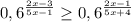
Показательная функция с основанием (0 <0,6 <1) убывающая, значит большему значению функции соответствует меньшее значение аргумента
Это означает, что в неравенстве между показателями степеней знак меньше:
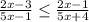
Получили дробно- рациональное неравенство.
Переносим выражение справа в левую часть
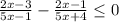
Приводим к общему знаменателю и получаем неравенство
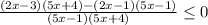
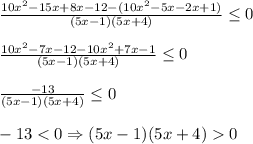
Знаменатель дроби не должен равняться 0, поэтому неравенство строгое.
Решение неравенства x < -4/5 или x>1/5
Интервалов два:
(-∞;-4/5) U (1/5;+∞)
Наименьшее целое положительное х=1
В ответ не вошли числа принадлежащие
[-4/5;1/5]
Далее непонятен вопрос, сумму каких чисел надо найти:
целых положительных?
Пошаговое объяснение:
В условии не указано расположение точек.
Случай 1.
Все четыре точки лежат на одной прямой.
Тогда через любые три из них, т.е. через прямую, можно провести бесчисленное множество плоскостей.
Случай 2.
Три точки равсположены на одной прямой, четвертая не лежит на той прямой.
Через прямую и точку, не лежащую на ней, можно провести плоскость, притом только одну.
Случай 3.
Ни одни три точки из четырех не расположены на одной прямой.
Через любые три точки можно провести плоскость, притом только оду.
а) Через точки 1,2,3 можно провести одну плоскость. б) Через точки 1,2,4 можно провести вторую плоскость. в) через точки 1,3,4 можно провести третью плоскость. г) через точки 2,3,4 можно провести четвертую плоскость.
Т.е. при таком расположении точек можно провести четыре плоскости.