Сейчас ? час; 8 час назад , до п/дня в 2 р < ,чем сейчас до п/ночи↓; сейчас до п/ночи ? час.решение. полдень - в 12 час, полночь - в 24 час; х время "сейчас"; (24 - х время до сегодняшней полуночи; х - 8 время 8 часов назад; 12 - (х-8) = (20 - х) время до полдня; (24 - х) = 2 * (20 - х) по условию; 24 - х = 40 - 2х; 2х - х = 40 - 24; х = 16 (час) это время сейчас. 24 - х = 8(час) время до полуночи. ответ: до сегодняшней полуночи осталось 8 часов. проверка: 8 час назад было 16-8=8(часов), до полдня оставалось 12-8=4(часа). 8: 4=2; 2=2, т.е. "сейчас" время до полуночи действительно в два раза больше, чем 8 час назад до полдня!
1. По теореме Бернулли, p = 0,8; q = 1-p = 0,2 1) Вероятность, что 4 мотора работает, а 2 не работает. P(4) = C(4, 6)*p^4*q^2 = 6*5/2*(0,8)^4*(0,2)^2 = 0,24576 2) Вероятность, что работают все 6 моторов P(6) = C(6, 6)*p^6*q^0 = 1*(0,8)^6*1 = 0,262144 3) Вероятность, что работает не больше 2 моторов, то есть 0 или 1. P(0) = C(0, 6)*p^0*q^6 = 1*1*(0,2)^6 = 0,000064 P(1) = C(1, 6)*p^1*q^5 = 6*(0,8)^1*(0,2)^5 = 0,001536 Общая вероятность равна сумме этих двух P = P(0) + P(1) = 0,000064 + 0,001536 = 0,0016
4. По той же формуле Бернулли, p = 0,4; q = 1-p = 0,6. Вероятность, что событие А появится меньше 2 раз из 6, то есть 0 или 1. P(0) = C(0, 6)*p^0*q^6 = 1*1*(0,6)^6 = 0,046656 P(1) = C(1, 6)*p^1*q^5 = 6*(0,4)^1*(0,6)^5 = 0,186624 Общая вероятность, что А наступит МЕНЬШЕ 2 раз P = P(0) + P(1) = 0,046656 + 0,186624 = 0,23328 Вероятность того, что А наступит НЕ МЕНЬШЕ 2 раз, и значит, в результате наступит событие В. Q = 1 - P = 1 - 0,23328 = 0,76672
9,2
Пошаговое объяснение:
9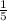 =9,2
=9,2