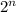 (n строго больше 1) элементов проиграет, а тот, кому попалась кучка с числом камней, не равным степени 2 - выигрывает.
(n строго больше 1) элементов проиграет, а тот, кому попалась кучка с числом камней, не равным степени 2 - выигрывает.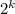 камней - проигрывает, а
камней - проигрывает, а 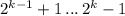 - выигрывает. Докажем, что тот, кому выпало
- выигрывает. Докажем, что тот, кому выпало 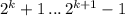 камней выиграет, а тот, кому выпало
камней выиграет, а тот, кому выпало 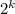 камней - проиграет.
камней - проиграет.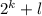 камней,
камней, 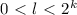 . Тогда мы можем взять эти l камней. Дейтсвительно, из того, что
. Тогда мы можем взять эти l камней. Дейтсвительно, из того, что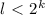
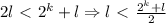
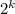 камней и, по предположению индукции, проигрывает
камней и, по предположению индукции, проигрывает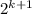 камней. Тогда можно взять любое количество от 1 до
камней. Тогда можно взять любое количество от 1 до 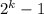 (так как
(так как 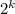 ровно в 2 раза меньньше, чем
ровно в 2 раза меньньше, чем 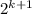 , а по условию можно взять строго меньше, чем в 2 раза). Тогда мы получим кучку с количеством камней от
, а по условию можно взять строго меньше, чем в 2 раза). Тогда мы получим кучку с количеством камней от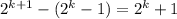
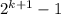
12:5
Пошаговое объяснение:
проведем МЛ паралельно ВС. Пусть Н - пересечение МЛ и А К. Треугольник МНК равен треугольнику КВР (по стороне и двум углам к ней прилежащим).
Его площадь 1/6 площади АВМ и значит 1/12 площади АВС.. Площадь АВМ равна половине АВС.
Значит ,искомая площадь 1/2-1/12, т.е. 5/12 площади всего треугольника АВС,